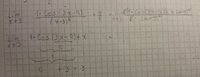What's the answer to this indeterminated limit?

[AngeloBenjamin0]

The excercises says that in order to

\begin{equation*}
g( x) =\frac{1-Cos( 3x-9)}{( x-3)^{2}} +\frac{x}{6}
\end{equation*}

be continuos in X=3, then g(3) should be...

I understand that for a function to be continuos in a point, the limit should be equal to evaluate the function in that point. I solved this in two different ways and both give me different answers.
The graphic is hard to analize, so I can't get an answer from there. I appreciate the help, thanks.

 

[Dr.Peterson]

Your first (short) attempt is wrong because you "canceled" in a way that makes no sense. You can't cross out a different factor of each term; what you did amounts to just ignoring the original denominators.

In the second, you at least started with the right idea, but it is hard to follow, and I think you lost some pieces along the way. In particular, the x/6 seems to have disappeared, and the sin^2 was split up in a way that didn't help. I would try to get it in the form [sin(something)/(something)]^2.