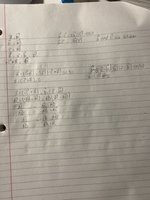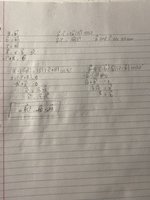johnnyluvsmath
New member
- Joined
- Jan 13, 2021
- Messages
- 17
Hi, there’s this question I’ve been stuck on for a while now. I started it but I’m not sure where to go from there. Here is the question and here’s what I did, although I’m sure it’s completely wrong. I would appreciate it if someone could give me a few clues so I can solve the problem.