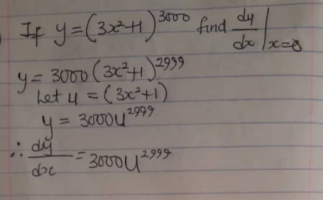If y = (3x^2+1)^3000, find dy/dx| x=0
- Thread starter ugu
- Start date
which is correct then?
Harry_the_cat
Elite Member
- Joined
- Mar 16, 2016
- Messages
- 3,784
It is your notation that is incorrect. Where is dy/du and du/dx ?
Also, have another look at your last line. What is 6(0) ?
Also, have another look at your last line. What is 6(0) ?
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
[imath]y = {\left( {3{x^2} + 1} \right)^{3000}},\quad {\left. {\dfrac{{dy}}{{dx}}} \right|_{x = 0}}[/imath], This is exactly what was posted.
My question to ugudansam is: why not simply use to chain rule in one step?
[imath] \dfrac{dy}{dx}=3000\left(3x^2+1\right)^{2999}\left(6x\right)=18000x\left(3x^2+1\right)^{2999}~.[/imath]
Is it not clear now what the value of the derivative at [imath]x=0 \text{ is }~?[/imath]
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,854
There are several ways you can apply the chain rule; using u as you evidently have been taught is valid (though you are expected to outgrow it). But you have to do it carefully. Here you made several mistakes, from writing y on the second line when you surely meant y', to leaving off the derivative of u in the last line.
Here is one page that (near the bottom) differentiates a function twice, once using f(g(x)) notation, and again using your form with u:
Derivative Rules
The Derivative tells us the slope of a function at any point. There are rules we can follow to find many derivatives.
www.mathsisfun.com
Here is another that teaches something more like pka's approach, which is mine:
Calculus I - Chain Rule
In this section we discuss one of the more useful and important differentiation formulas, The Chain Rule. With the chain rule in hand we will be able to differentiate a much wider variety of functions. As you will see throughout the rest of your Calculus courses a great many of derivatives you...
tutorial.math.lamar.edu
And the following page starts with many examples using your approach, then transitions to the more mature "direct" approach at the end (part 5):
When I teach this, I draw a box around the "inside" part (your u) and suggest thinking of that as if it were a variable, differentiating, and then multiplying by the derivative of what's in the box.
ok sir, i will check to see and try adjusting the mistakesThere are several ways you can apply the chain rule; using u as you evidently have been taught is valid (though you are expected to outgrow it). But you have to do it carefully. Here you made several mistakes, from writing y on the second line when you surely meant y', to leaving off the derivative of u in the last line.
Here is one page that (near the bottom) differentiates a function twice, once using f(g(x)) notation, and again using your form with u:
Derivative Rules
The Derivative tells us the slope of a function at any point. There are rules we can follow to find many derivatives.www.mathsisfun.com
Here is another that teaches something more like pka's approach, which is mine:
Calculus I - Chain Rule
In this section we discuss one of the more useful and important differentiation formulas, The Chain Rule. With the chain rule in hand we will be able to differentiate a much wider variety of functions. As you will see throughout the rest of your Calculus courses a great many of derivatives you...tutorial.math.lamar.edu
And the following page starts with many examples using your approach, then transitions to the more mature "direct" approach at the end (part 5):
When I teach this, I draw a box around the "inside" part (your u) and suggest thinking of that as if it were a variable, differentiating, and then multiplying by the derivative of what's in the box.
I agree that as you gain experience you will use u-substitutions less frequently and that you will use the chain rule without intermediate steps. But
[math]\text {Given } y = (3x^2 + 1)^{3000}, \text { find } \dfrac{dy}{dx} \text { at } x = 0.[/math]
Start by finding dy/dx. If you use a u-substitution, that means
[math]\dfrac{dy}{dx} = \dfrac{dy}{du} * \dfrac{du}{dx}.[/math]
[math]u = 3x^2 + 1 \implies \dfrac{du}{dx} = 6x \text { and } y = u^{3000}.[/math]
[math]y = u^{3000} \implies \dfrac{dy}{du} = 3000u^{2999}.[/math]
[math]\therefore \dfrac{dy}{dx} = \dfrac{dy}{du} * \dfrac{du}{dx} = 3000u^{2999} * 6x = 18000x(3x^2 + 1)^{2900}.[/math]
Now substitute 0 for x. What do you get?
Your method works if you follow it carefully.
[math]\text {Given } y = (3x^2 + 1)^{3000}, \text { find } \dfrac{dy}{dx} \text { at } x = 0.[/math]
Start by finding dy/dx. If you use a u-substitution, that means
[math]\dfrac{dy}{dx} = \dfrac{dy}{du} * \dfrac{du}{dx}.[/math]
[math]u = 3x^2 + 1 \implies \dfrac{du}{dx} = 6x \text { and } y = u^{3000}.[/math]
[math]y = u^{3000} \implies \dfrac{dy}{du} = 3000u^{2999}.[/math]
[math]\therefore \dfrac{dy}{dx} = \dfrac{dy}{du} * \dfrac{du}{dx} = 3000u^{2999} * 6x = 18000x(3x^2 + 1)^{2900}.[/math]
Now substitute 0 for x. What do you get?
Your method works if you follow it carefully.