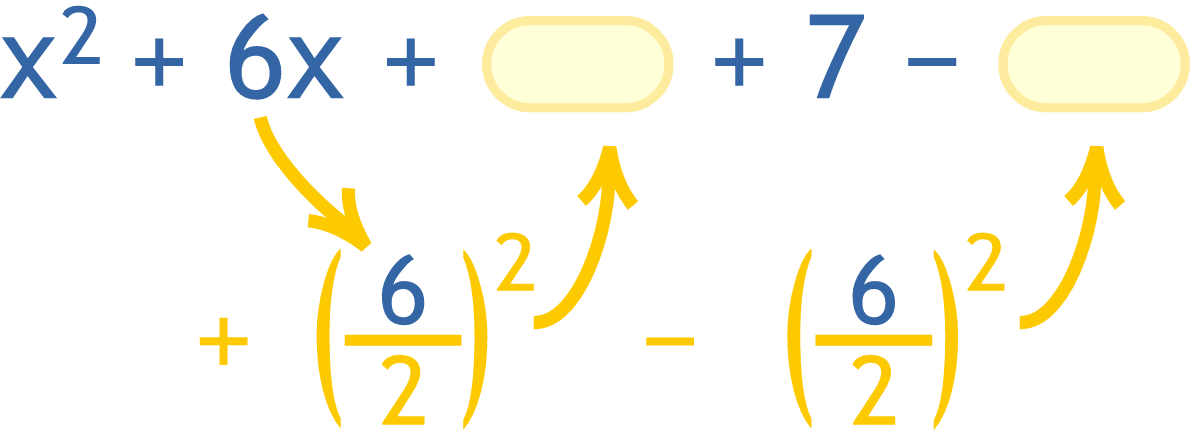100 Integrals

[nasi112]

I'm watching the video 100 Integrals of blackpenredpen. I'm on number 28 at time 1:35:00.

[imath]\displaystyle \int \sqrt{x^2 + 4x + 13} \ dx = \int \sqrt{(x + 2)^2 + 3^2} \ dx[/imath]

What is the strategy to go from [imath]x^2 + 4x + 13[/imath] to [imath](x + 2)^2 + 3^2[/imath]?

 

[Dr.Peterson]

That's called completing the square. See here for an explanation:

Calculus II - Integrals Involving Quadratics

In this section we are going to look at some integrals that involve quadratics for which the previous techniques won’t work right away. In some cases, manipulation of the quadratic needs to be done before we can do the integral. We will see several cases where this is needed in this section.

tutorial.math.lamar.edu

Completing the Square

Completing the Square is where we ... But if you have time, let me show you how to Complete the Square yourself.

www.mathsisfun.com

 

[fresh_42]

What is the strategy to go from [imath]x^2 + 4x + 13[/imath] to [imath](x + 2)^2 + 3^2[/imath]?

The idea is that we can now substitute [imath] y=x+2 [/imath] with [imath] dx=dy [/imath] and get a more standard integral [math] \int\sqrt{y^2+3^2}\,dy .[/math]Here are some lists of integral formulas:

Formelsammlung Mathematik: Unbestimmte Integrale algebraischer Funktionen – Wikibooks, Sammlung freier Lehr-, Sach- und Fachbücher

de.wikibooks.org

 

[nasi112]

Thanks.

 

[khansaheb]

The idea is that we can now substitute [imath] y=x+2 [/imath] with [imath] dx=dy [/imath] and get a more standard integral [math] \int\sqrt{y^2+3^2}\,dy .[/math]Here are some lists of integral formulas:

Formelsammlung Mathematik: Unbestimmte Integrale algebraischer Funktionen – Wikibooks, Sammlung freier Lehr-, Sach- und Fachbücher

de.wikibooks.org

To continue this integration, substitute
y →3* tan(Ø)→ dy = 3*sec^2 (Φ)
and
y^2 + 3^2 = 3^2 * [1+tan^2(Φ)]..... and continue.....

 

[lookagain]

To continue this integration, substitute
y →3* tan(Ø)→ dy = 3*sec^2 (Φ)

[imath] dy \ = \ 3sec^2(\theta) \ d(\theta) [/imath]

 

[khansaheb]

[imath] dy \ = \ 3sec^2(\theta) \ d(\theta) [/imath]

Correct - my mistake. I was wrong.