sumit saurav
New member
- Joined
- Jan 6, 2014
- Messages
- 14
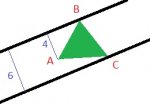
ABC is an equilateral triangle such that the vertices B and C lie on two parallel lines at a distance 6. if A lies between the parallel lines at a distance 4 from one of them,then the lenght of a side of the equilateral triangle is:
a) 8
b) whole under root 88/3
c)4 under root 7/under root 3
d) none of these
i dont get the meaning that at a distance 6?
a) 8
b) whole under root 88/3
c)4 under root 7/under root 3
d) none of these
i dont get the meaning that at a distance 6?
Last edited: