Angles of a pentagon

[johndoe]

Hello!

I've been bashing my head with this problem for the past couple of days and I'm starting to get the feeling there might not be a solution although my intuition tells me otherwise.

So basically I have this irregular pentagon (picture here: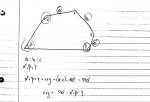 ) and I know all the circled parameters (angles alpha, beta and gamma and the ratio of three of its sides a:b:c). The goal here is to find the other two angles x and y.

I know about the sum of all internal angles of a polygon, so I know x+y=540-alpha-beta-gamma. I've forming all sorts of triangles but I never derive another connection. My 'intuition' is that once I have the initial three angles fixed (known) I cannot build the sides a, b and c with the specified ratio anywhere else apart from one place. If you don't understand the above explanation - it does not matter as that is just my reasoning that the supplied information is enough to find the unknown angles.

The solution that I derived (picture here: ) is slightly dodgy looking as I end up with x being function of only beta and alpha and I feel that can't be true. Just an explanation to what I've done - I've extended the sides to create a triangle and used law of cosines and law of sines to end up with a trigonometric equation that has only known angles, finally I combine that with the initial x+y=540-the_three_known_angles equation and solve them (using Maple) to get the dodgy result of x=f(beta, alpha).

Has anyone seen anything similar before? Any thoughts on my solution? Any thoughts on my 'intuition' and the fact there might not be a solution due to the lack of information given?

 

[Dale10101]

Small idea offered

Hi

Hope you are not feeling ignored, possibly Geometry is not so many peoples long suit. I have played with your problem a little and can not see how you can accomplish your goal right off.

If I had more time I think I would start adding construction lines between the vertices and dropping/drawing lines from a vertice to an opposite sides to form right triangles. My goal would be to see if I could find the necessary angles to calculate the perimeter going clockwise, and then counter clock wise to find if the resulting equations plus the sum of the interior angle equation might provide a solution. This is really just a half an idea, an avenue of exploration.

Interesting problem wish I had more time to play with it, good luck.

PS. Oh, have you checked out http://www.geogebra.org/cms/en/, fabulous free program that allows construction of Geometrical figures and the means to vary sides and angles while getting read outs of how such changes effect the other parameters plus tons more. You might draw a pentagon and then start varying the side and angles, I think you could even put in conditions restricting the ratio of the lengths of certain sides. Using the program does have a steep learning curve however. My thought there is to provide a mechanical means of exploring whether your problem does indeed have sufficient information to find the solution that you seek ... and it is a fun program that might help you explore other Geometry problems. Too bad we all don't live to be a 1000.

 

[johndoe]

Thread resolution

Thanks for the reply, Dale10101!

I have also posted my question on another Maths forum in hopes of more people seeing it (http://www.mymathforum.com/viewtopic.php?f=13&t=45850). User Denis replied with "For a n sided polygon, you need all the angles IN ORDER and
n−2 consecutive side lengths in order to construct the polygon.", which was taken from this math stack exchange http://math.stackexchange.com/quest...f-an-irregular-polygon-when-all-interior-angl.

I do not have further information or proof why that is the case but after several days of tireless construction of external or internal triangles and trying to solve them in any way possible I am convinced it is true. As I needed the solution of that problem for a project of mine, I will just have to slightly redesign some stuff, so that I know 4 angles - that would make the problem possible to solve (as you can still find the fifth one from subtracting the other four from the total sum of the angles).

The program you provided seems really fun to play with! I'm gonna keep it as I might need it some day! It kinda looks like the application you were looking (for 3D plotting) but in 2D instead. I use an app, Grapher, that is built in MacOS but it's Mac exclusive I'm afraid - if you ever come to use a Mac and still need to do 2D or 3D plots (they can intersect as well, yay!), you can give it a try! (Or you might be feeling adventurous and decide to partition your hard drive and switch to Hackintosh haha ) And one last thing - a quick google search for apps similar to Grapher led me to Microsoft Mathematics 4.0 (http://www.microsoft.com/en-gb/download/details.aspx?id=15702) - I'm not sure if it's free or if it's gonna be of any use to you, but you can check it out if you feel like it.


Moderator Note: I approved this post, as the Microsoft application appears to be free of charge. This product has not been reviewed; install at your own risk.

 

[Dale10101]

Great

Thanks for the reply, Dale10101!

.... And one last thing - a quick google search for apps similar to Grapher led me to Microsoft Mathematics 4.0 (http://www.microsoft.com/en-gb/download/details.aspx?id=15702) - I'm not sure if it's free or if it's gonna be of any use to you, but you can check it out if you feel like it.


Moderator Note: I approved this post, as the Microsoft application appears to be free of charge. This product has not been reviewed; install at your own risk.

Glad you have your math problem in hand. Micro. math does allow the simultaneous graphing of two 3-D equations, very cool. Thanks for the link.

 

[johndoe]

Last post.

Hey guys!

Just thought I should show you what I've been doing. This is a prototype for a VR glove that currently has only one finger "working". I thought I could calculate the angles of two of the joints by knowing the rest but maths proves that impossible, so I just added another sensor and it's working. The animation finger looks crooked mainly because the virtual palm does not rotate at all and my real one does, so that introduces a lot of error to the finger. I'm adding another sensor to the palm so hopefully that's gonna fix some of the 'crookedness'. (Some because another portion is due to the not-so-perfect Kalman filter I'm using but that's gonna take a lot of time to fix and is not a priority for now )

Thanks again to all that helped!