Application of Trigonometry: Emma is 90m due west of Michele on a level road....

[writer2019]

Hey Guys,
I'm doing math and I'm really stuck on a question. It is:
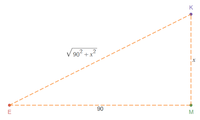
Emma is 90m due west of Michele on a level road. Emma sees the angle of elevation of the kite flown by RIley at 30 degrees, while Michele sees that it is due north at an angle of elevation of 38 degrees. What is the height of the kite?

I've tried drawing 3D models, 2D traingles etc, but I still can't solve it. I will scan and attach my working out really soon.

 

[MarkFL]

Hello, and welcome to FMH!

Consider the following diagram:


E and M mark the locations of Emma and Michelle respectively, and K marks the spot on the ground over which the kite is directly flying, at height \(h\). Now, from the information given in the problem, we may write:

[MATH]\tan\left(38^{\circ}\right)=\frac{h}{x}[/MATH]
[MATH]\tan\left(30^{\circ}\right)=\frac{h}{\sqrt{90^2+x^2}}[/MATH]
You now have two equations in two unknowns...can you proceed?

 

[MarkFL]

To follow up:

Write the 2nd equation as:

[MATH]\frac{1}{\sqrt{3}}=\frac{h}{\sqrt{90^2+x^2}}[/MATH]
Invert both sides:

[MATH]\sqrt{3}=\frac{\sqrt{x^2+90^2}}{h}[/MATH]
Or:

[MATH]\sqrt{3}h=\sqrt{x^2+90^2}[/MATH]
Now, the first equation implies:

[MATH]x=h\cot\left(38^{\circ}\right)[/MATH]
Substitute for \(x\):

[MATH]\sqrt{3}h=\sqrt{\left(h\cot\left(38^{\circ}\right)\right)^2+90^2}[/MATH]
Square both sides:

[MATH]3h^2=h^2\cot^2\left(38^{\circ}\right)+90^2[/MATH]
Arrange as:

[MATH]3h^2-h^2\cot^2\left(38^{\circ}\right)=90^2[/MATH]
Factor the LHS:

[MATH]h^2\left(3-\cot^2\left(38^{\circ}\right)\right)=90^2[/MATH]
Arrange as:

[MATH]h^2=\frac{90^2}{3-\cot^2\left(38^{\circ}\right)}[/MATH]
Thus we find \(h\) (in meters) to be:

[MATH]h=\frac{90}{\sqrt{3-\cot^2\left(38^{\circ}\right)}}\approx77.124775[/MATH]