Area of ( a part of ) the surface of a sphere problem

[Ognjen]

Official problem formulation:

Calculate the part of the surface of a sphere which is seen from point A if the radius of the sphere is r, and the distance between point A and the center of the sphere is d ( d > r ).

The confusion on my part pertains to 2 things, which I will note below.

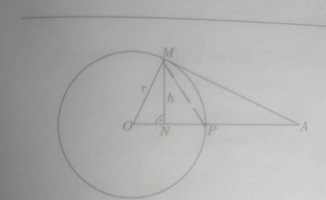
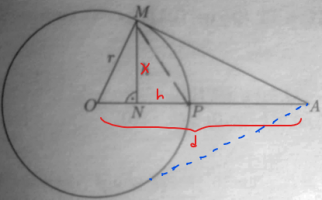
First comes with the official visualization of the problem presented on the picture below. Why is A not defined as the intersection of 2 tangent lines on the circle ? This was my first intuitive assumption ( possibly derived from analytic geometry, but also quite logical when I think about the way humans see things, in their whole ) ), but it ended up being false, as shown below. Why ?

The official solution then proceeds to utilize similarity of triangles OAM and ONM in the following manner:

[math]\frac{ON}{OM} = \frac{OM}{OA}[/math][math]ON = \frac{OM^2}{OA} = \frac{r^2}{d}[/math]
Now comes the second confusing part for me.

The official solution now says ( with no explanation ) that:

[math]h = NP = OP - ON = r - \frac{r^2}{d} = r(1 - \frac{r}{d} )[/math]
I don't at all understand how they concluded that h equals NP. I assume it is related to the face OPM is an isosceles triangle ( because OP and OM are both radii of the sphere ), but I cannot determine exactly how h = NP is deduced from this fact.

Any help would be highly appreciated.

 

[Dr.Peterson]

First comes with the official visualization of the problem presented on the picture below. Why is A not defined as the intersection of 2 tangent lines on the circle ? This was my first intuitive assumption ( possibly derived from analytic geometry, but also quite logical when I think about the way humans see things, in their whole ) ), but it ended up being false, as shown below. Why ?

Certainly A is the point of intersection of two tangents (though that's not its definition -- it's defined by the problem as a point d units from O). Since you have to use d, you can't use only the tangents in solving the problem.

But why do you say your assumption is false?? No one is denying it; they just choose to draw only one of the tangents, because that's all we need.

The official solution now says ( with no explanation ) that:

[math]h = NP = OP - ON = r - \frac{r^2}{d} = r(1 - \frac{r}{d} )[/math]
I don't at all understand how they concluded that h equals NP. I assume it is related to the face OPM is an isosceles triangle ( because OP and OM are both radii of the sphere ), but I cannot determine exactly how h = NP is deduced from this fact.

Certainly these authors are rather terse (which is not unusual, though we can wish otherwise).

They've also clearly labeled the diagram incorrectly, since the h there is MN, not NP as they've defined it in their work. You need to correct that on the drawing while working through their answer!

​

Authors can make mistakes, just as you and I can. You have to take that into account in any communication, even reading a textbook. If something is obviously wrong, go with what you know.