logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
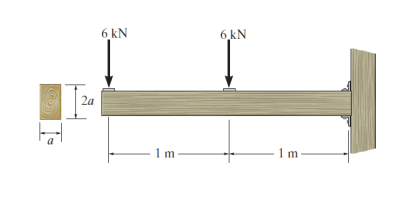
Determine the minimum dimension \(\displaystyle a\) to the nearest \(\displaystyle \text{mm}\) of the beam’s cross section to safely support the load. The wood has an allowable normal stress of \(\displaystyle \sigma_{\text{allow}} = 10 \ \text{MPa}\) and an allowable shear stress of \(\displaystyle \tau_{\text{allow}} = 1 \ \text{MPa}\).