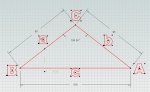
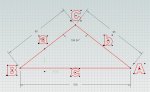
Sorry....I have been out of school for over 45 years and I wasn't very good at trig even then. I have attached a diagram showing what I am talking about. Basically, in the diagram (ignore the dots...artifact of the software), I show an angle of 104.34 degrees for angle C. I knew this was close, but not exactly correct for a c of 150mm, so.....
I took the standard law of cosines .... COS(C) = (a2+b2-c2)/2ab
and since the a and b were of equal length, I ignored b and came to ... COS(C)=(2a2-c2)/2a2
... or ... COS(C)= -c2/2a2 This line is like saying (5-2)/5 = -2/5, which is not true. This is why you should NOT say that things cancel out. You can say things cancel out to 1 or things cancel out to 0 but not just things cancel out!
... or ... COS(C) = -0.67036 The only way you can say exactly what -c2/2a^2 is if you know what a and c are. You told us that a is 95 but what is c? Your own answer above will only be correct if c ~ 110, yet your own diagram shows that c=150
....so ....COS-1(0.67036) = 1.819905 rad
... or ... 104.2729 deg
end result: angle C = 104.2729 degrees.
I think this would yield a formula for calculating the angle for any given c of... Angle C in degrees = COS-1(-c2/18050 ) * 57.2957795 .... assuming that a and b will always be 95mm and fixed.
I think this is right, but not sure if there is a better way to do this.
Thanks for your response and any further assistance you might see fit to provide.
Charlie