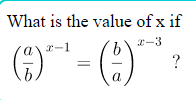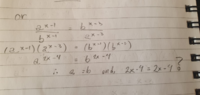Can't figure out what i am doing wrong - Laws of exponent

[Unit_02]

The problem:




I cannot find whats wrong with my method. I understand the solution below but i tried a different approach and got stuck.

My approach:



Why am i not able to solve it like that? Am i missing something or doing something wrong?

That's the solution given:

 

[Harry_the_cat]

Basically you have shown that the statement is true if a=b. That is, if a=b, then x can be anything.
That makes sense! Because if a=b then a/b = 1 and b/a = 1 and it's true that 1^(x-1) = 1^(3-x) for any value of x.

So, if a=b, x can be anything. But if a\(\displaystyle \neq\)b, then x=2.

 

[Unit_02]

Basically you have shown that the statement is true if a=b. That is, if a=b, then x can be anything.
That makes sense! Because if a=b then a/b = 1 and b/a = 1 and it's true that 1^(x-1) = 1^(3-x) for any value of x.

So, if a=b, x can be anything. But if a\(\displaystyle \neq\)b, then x=2.

I see my mistake now. But at first sight i couldn't tell if i was doing the steps correctly in order to solve the problem or not. Is there a way / steps to avoid this type of "mistake" while trying to solve a problem like this? Because in my mind i was developing towards the that "a" was not equal to "b"

 

[lev888]

I see my mistake now. But at first sight i couldn't tell if i was doing the steps correctly in order to solve the problem or not. Is there a way / steps to avoid this type of "mistake" while trying to solve a problem like this? Because in my mind i was developing towards the that "a" was not equal to "b"

Your solution is fine as long as you don't immediately conclude that a=b.
If a^2x-4 = b^2x-4
1. If a≠b, then 2x-4 must be 0, therefore, x = 2
2. If a=b, then x can be anything.

 

[Harry_the_cat]

When you have a statement like \(\displaystyle a^n = b^n\), the conclusion is EITHER a=b OR n=0. You left out the second conclusion.

 

[Unit_02]

Your solution is fine as long as you don't immediately conclude that a=b.
If a^2x-4 = b^2x-4
1. If a≠b, then 2x-4 must be 0, therefore, x = 2
2. If a=b, then x can be anything.

When you have a statement like \(\displaystyle a^n = b^n\), the conclusion is EITHER a=b OR n=0. You left out the second conclusion.

Thank you very much! I see it clearer now!

 

[lookagain]

Your solution is fine as long as you don't immediately conclude that a=b.
If a^2x-4 = b^2x-4
1. If a≠b, then 2x-4 must be 0, therefore, x = 2
2. If a=b, then x can be anything.

And neither a or b can equal 0.