Hello,
I stumbled upon a method of integral solving in which we change the coordinates in order to simplify calculations, here is an example:
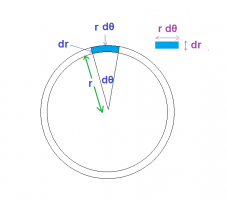
[math]\int\int_{D}\sqrt{x^2 + y^2 +1} dxdy = \int\int_{D}\sqrt{r^2cos^2(\theta) + r^2sin^2(\theta) + 1} \cdot rdr d\theta[/math]In the above integral I don't understand why finally, after the square root we multiply by [imath]\cdot r drd\theta[/imath] instead of bare [imath]drd\theta[/imath] as we did for [imath]dxdy[/imath].
Thanks
I stumbled upon a method of integral solving in which we change the coordinates in order to simplify calculations, here is an example:
[math]\int\int_{D}\sqrt{x^2 + y^2 +1} dxdy = \int\int_{D}\sqrt{r^2cos^2(\theta) + r^2sin^2(\theta) + 1} \cdot rdr d\theta[/math]In the above integral I don't understand why finally, after the square root we multiply by [imath]\cdot r drd\theta[/imath] instead of bare [imath]drd\theta[/imath] as we did for [imath]dxdy[/imath].
Thanks