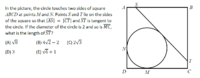
circle touches 2 sides of square ABCD at M, N; S, T lie on sides so |AS| = |CT|, ST tangent to circle
- Thread starter ssolaming
- Start date
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
It's probably "overkill" but I would set up a coordinate system with (0, 0) at the left bottom corner of the square. Yes, each side of the square has length "3" so the vertical side on the left has equation x= 3 and the horizontal side at the top has equation y= 3. The circle has diameter 2 so radius 1, its center is at (1, 1), and its equation, in this coordinate system, is \(\displaystyle (x- 1)^2+ (y- 1)^2= 1\). Take the point of tangency to be \(\displaystyle (x_0, y_0)\). Then a radius from the center of the circle to that point has slope \(\displaystyle \frac{y_0- 1}{x_0- 1}\). The line tangent to the circle has slope \(\displaystyle -\frac{x_0- 1}{y_0- 1}\) and its equation is \(\displaystyle y= -\frac{x_0- 1}{y_0- 1}(x- x_0)+ y_0\).
That tangent line will cross the right side of the square, x= 3, where \(\displaystyle y= -\frac{x_0- 1}{y_0- 1}(3- x_0)+ y_0\) so at \(\displaystyle T= \left(3, -\frac{x_0- 1}{y_0- 1}(3- x_0)+ y_0\right)\).
It will cross the top of the square, y= 3, where \(\displaystyle 3= -\frac{x_0- 1a}{y_0- 1}(x- x_0)+ y_0\) so that \(\displaystyle \frac{x_0- 1}{y_0- 1}(x- x_0)= y_0- 3]tex], \(\displaystyle x- x_0= \frac{y_0- 1}{x_0- 1}(y_0- 3)\) and \(\displaystyle x= x_0+ \frac{y_0- 1}{x_0- 1}(y_0- 3)\). \(\displaystyle S= \left(x_0+ \frac{y_0- 1}{x_0- 1}(y_0- 3), 3\right)\).
The length of line segment ST is the distance between those two points. I see no easy way to write that. In particular, that length, as one would expect from the picture, depends on exactly where we take the point of tangency, \(\displaystyle (x_0, y_0)\).\)
That tangent line will cross the right side of the square, x= 3, where \(\displaystyle y= -\frac{x_0- 1}{y_0- 1}(3- x_0)+ y_0\) so at \(\displaystyle T= \left(3, -\frac{x_0- 1}{y_0- 1}(3- x_0)+ y_0\right)\).
It will cross the top of the square, y= 3, where \(\displaystyle 3= -\frac{x_0- 1a}{y_0- 1}(x- x_0)+ y_0\) so that \(\displaystyle \frac{x_0- 1}{y_0- 1}(x- x_0)= y_0- 3]tex], \(\displaystyle x- x_0= \frac{y_0- 1}{x_0- 1}(y_0- 3)\) and \(\displaystyle x= x_0+ \frac{y_0- 1}{x_0- 1}(y_0- 3)\). \(\displaystyle S= \left(x_0+ \frac{y_0- 1}{x_0- 1}(y_0- 3), 3\right)\).
The length of line segment ST is the distance between those two points. I see no easy way to write that. In particular, that length, as one would expect from the picture, depends on exactly where we take the point of tangency, \(\displaystyle (x_0, y_0)\).\)
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,854
I would start by drawing a radius to each point of tangency, from which I could determine where the line is tangent to the circle (essentially, its coordinates). Then I might determine how far that point is from the top and right sides, and finish up by focusing on the upper right triangle. I do get one of the given choices, without much work.