conic section
- Thread starter Leons
- Start date
Harry_the_cat
Elite Member
- Joined
- Mar 16, 2016
- Messages
- 3,784
Where are you stuck? Are you given a specific point P?
I stuck after I find the slope. The question does not given a specific point P.
this is the slope that I get : [math](x-a)/2a[/math]
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
As I read the problem, the point P is specified by a parameter t, namely P [imath](a+2at, at^2)[/imath].
You are to find the slope at that point; your slope is correct as a function of x, so replace x with [imath]a+2at[/imath]. (The result is interesting!) Then find the equation of the line with that slope through that point.
can you check whether my answer is correct or not?
slope when x=a+2at
[math]\frac{a+2at-a}{2a}=t[/math]slope=t
tangent equation,[math](y-y_1)=m(x-x_1)[/math][math](y-at^2)=t(x-(a+2at))[/math][math]y=tx-at-2at^2+at^2[/math][math]y=tx-at-at^2[/math]
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
Yes, that's correct. As confirmation, I've graphed the parabola and the line:
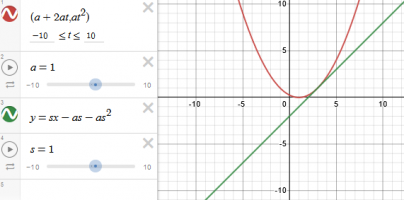
Here, t is the parameter for drawing the curve, and s is a particular value of t to determine the point.
thank you so much
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
hairy conic??
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
i still dont understand?.. what does relate with him
i already got the equation of tangent and parabola which are
[math]y=tx-at-at^2[/math][math]ty+x=a+2at+at^3[/math]
now i stuck at this question ,,
if the normal and tangent line across x-axis at point T and N respectively, show that
[math]\frac{PT^2}{TN}=at[/math]
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
Please show whatever you have tried for this part. The points T and N are the x-intercepts of your two lines. How do you find those?
tangent line at point N
[math]0=tx-at-at^2[/math]Normal line at point T
[math]0=a+2at+at^3-x[/math]
im a bit confused, whether i have to prove on the left hand side or right hand side
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
okay i will try solve that, please check for me
Point T:
[math]x=\frac{at+at^2}{t}[/math]Coordinate point T :[math](\frac{at+at^2}{t},0)[/math]Point N:
[math]x=a+2at+at^3[/math]Coordinate point N
[math](a+2at+at^3,0)[/math]Coordinate point P
[math](a+2at,at^2)[/math]
distance PT:
[math]\sqrt{(a+2at-(\frac{at+at^2}{t}))^2+(at^2-0)^2}[/math][math]\sqrt{a^2t^2+a^2t^4}[/math][math]PT^2=a^2t^2+a^2t^4[/math]
distance TN:
[math]\sqrt{(\frac{at+at^2}{t}-(a+2at+at^3))^2+(0-0)^2}[/math][math]TN=-at-at^3[/math]
so,
[math]\frac{PT^2}{TN}=\frac{a^2t^2+a^2t^4}{-at-at^3}=\frac{a^2t^2(1+t^2)}{-at(1+t^2)}=-at[/math]
i got -at,, what i know distance should be positive, so i want to ask whether i can change the sign or not?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
Since a distance is always positive, your expression for TN should have had an absolute value. (The square root of a square is the absolute value.)
So, yes, your final answer will be at, if a and t are positive! Was that stated in the problem? If not, the answer should really be [imath]|at|[/imath].
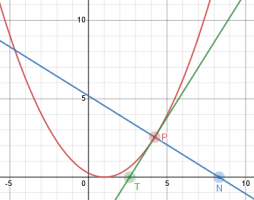
Also, since N is to the right of T when [imath]t>0[/imath], you might have subtracted T from N rather than N from T in your calculation, to avoid the absolute value. Here is a graph, for [imath]t=1.6[/imath]:
oh,, now i understand. Thank you so much !!