realVikash
New member
- Joined
- Apr 2, 2021
- Messages
- 4
Hi, I'm from NZ we use (x-x1)^2 and (y=y1)^2 in our general equations, so what do r represent, and in all our high schools we don't teach the 2 formulas you've given me. I also did what you said and don't understand how to continue. Thanks for the help.I would set the origin at the center of both ...
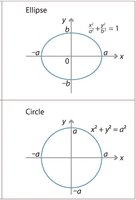
top half of circle ...
[MATH]y = \sqrt{r^2-x^2}[/math]
you are given [MATH]y[/MATH] and [MATH]r[/MATH], solve for the value of [MATH]x_P>0[/MATH]
top half of ellipse ...
[MATH]y = b\sqrt{1 - \frac{x^2}{a^2}}[/MATH]
you are given [MATH]y[/MATH], [MATH]a[/MATH], and [MATH]b[/MATH], solve for the value of [MATH]x_R>0[/MATH]
finding the horizontal distance should be straightforward