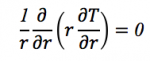Hi all,
Please could someone explain me how to get constants of Heat Diffusion Eq. for cylindrical coordinates step by step.
\(\displaystyle \dfrac{1}{r}\, \dfrac{\partial}{\partial r}\, \left(r\, \dfrac{\partial T}{\partial r}\right)\, =\, 0\)
Thanks a lot!
Please could someone explain me how to get constants of Heat Diffusion Eq. for cylindrical coordinates step by step.
\(\displaystyle \dfrac{1}{r}\, \dfrac{\partial}{\partial r}\, \left(r\, \dfrac{\partial T}{\partial r}\right)\, =\, 0\)
Thanks a lot!
Attachments
Last edited by a moderator: