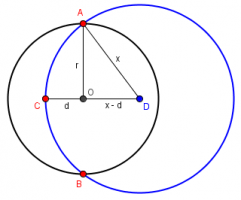
I would really appreciate some help on a geometry challenge I am facing. I don't expect the answer but rather some guidance on how to get there and the best method to use.
The problem I am facing is captured in the figure below:
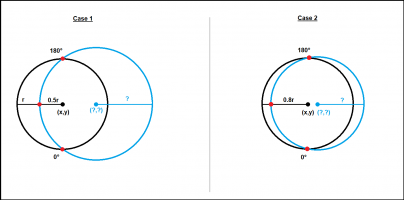
Let us first consider Case 1:
I am given a black circle. I know the central co-ordinates of the circle (x,y) and I know it's radius. I am then given two red points on the circumference of the black circle, which are 180° apart. I know the co-ordinates of these points too. I am then given a third red point that lies within the black circle, some distance along it's radius (in this case 0.5r along). I know the co-ordinates of this point as well.
The challenge: I need to construct a new circle, i.e. the blue one. The conditions of this circle are that it's circumference must pass precisely through the centre of all three red points. My assumption is that I need to find the blue circle's central co-ordinates and radius, but I have no idea how. Can anyone please advise how to go about this?
Let us also consider Case 2:
This is the same problem except that the red point within the black circle lies further along it's radius. The two red points are still on it's circumference and are still 180° apart; this will always be the case. Once again the challenge is to construct the new, i.e. blue circle. I can see that this circle will be smaller, and it seems reasonable that the further the red point on the black radius reaches the edge of the radius, the closer the blue circle gets to the original black one.
_
I will face other such scenarios where the inner red point on the black radius is at other lengths along it, so knowing the best method to solve the problem is really what I am after. Any guidance would be really appreciated and please let me know if anything is unclear?
N.B. The sketch is a rough approximation so please forgive any inaccuracies in lining up the points and lines.
The problem I am facing is captured in the figure below:

Let us first consider Case 1:
I am given a black circle. I know the central co-ordinates of the circle (x,y) and I know it's radius. I am then given two red points on the circumference of the black circle, which are 180° apart. I know the co-ordinates of these points too. I am then given a third red point that lies within the black circle, some distance along it's radius (in this case 0.5r along). I know the co-ordinates of this point as well.
The challenge: I need to construct a new circle, i.e. the blue one. The conditions of this circle are that it's circumference must pass precisely through the centre of all three red points. My assumption is that I need to find the blue circle's central co-ordinates and radius, but I have no idea how. Can anyone please advise how to go about this?
Let us also consider Case 2:
This is the same problem except that the red point within the black circle lies further along it's radius. The two red points are still on it's circumference and are still 180° apart; this will always be the case. Once again the challenge is to construct the new, i.e. blue circle. I can see that this circle will be smaller, and it seems reasonable that the further the red point on the black radius reaches the edge of the radius, the closer the blue circle gets to the original black one.
_
I will face other such scenarios where the inner red point on the black radius is at other lengths along it, so knowing the best method to solve the problem is really what I am after. Any guidance would be really appreciated and please let me know if anything is unclear?
N.B. The sketch is a rough approximation so please forgive any inaccuracies in lining up the points and lines.