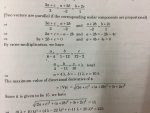Cross multiplication: specifically, (a/8-4 = B/1-12 = C/12-2 )

[R.K.4.7]

Hi guys can anyone please show me how is this question is done From the step ( By Cross Multiplication Method ....)

There are actually 3 terms that are equal...

The line that says
(a/8-4 = B/1-12 = C/12-2 )Is the only step i can't understand.
Please help
Thanks!

 

[tkhunny]

First of all, get the concept of "Cross Multiplication" OUT of your head. It WILL confuse you. Just learn to multiply.

Find common denominator and multiply. Why is that not a solution to your dilemma?

 

[R.K.4.7]

I have tried elimination method and substitution method I can't do it, I've even tried the multiplication method, but there is no denominator in any equation. How do I multiply without the denominator? Also how are the 2 equations seperated into 3 equal terms ? Very confusing!!

 

[tkhunny]

Are we looking at the same problem?

\(\displaystyle \frac{2a+c}{2} = \dfrac{a+2b}{-2} = \dfrac{b+2c}{-1}\)

There are three denominators in there.

Multiply by 2

\(\displaystyle 2a+c = -a-2b = -2b - 4c\)

There are three equations in there.

\(\displaystyle 2a+c = -a-2b\)
\(\displaystyle 2a+c = -2b-4c\)
\(\displaystyle -a-2b = -2b-4c\)

It is a bit unusual to work with three equations simultaneously. If you have a specific application where this turns out to be convenient, great. On the other hand, breaking it out to more familiar territory is always an option.

 

[R.K.4.7]

No, that is not the problem I'm facing.
Please explain this step :-

3a+2b+C=0 & a+4b+4c=0 .......stepA
By cross multiplication we have,
A/(8-4) = b/(1-12) = C/(12-2) ........stepB

The other steps are in the image I've attached which is in the first post. But I just need to understand how we go from stepA to stepB.

 

[mmm4444bot]

Why is that not a solution to your dilemma?

Because you misread the OP, tk. :cool:

The student was instructed to use cross-multiplication to go FROM:

3a + 2b + c = 0

a + 4b + 4c = 0

TO:

a/(8-4) = b/(1-12) = c/(12-2)

I do not understand what the instructor is talking about. I hope somebody else here does.

 

[R.K.4.7]

Because you misread the OP, tk. :cool:

The student was instructed to use cross-multiplication to go FROM:

3a + 2b + c = 0

a + 4b + 4c = 0

TO:

a/(8-4) = b/(1-12) = c/(12-2)

I do not understand what the instructor is talking about. I hope somebody else here does.

I'm afraid no one does ?...

 

[tkhunny]

Apparently, we need a "Cross Product" and it has NOTHING to do with "Cross Multiplication". Weird Translation?

The Cross Product produces <i(8-4),j(1-12),k(12-2)>.

This gives the result.

 

[R.K.4.7]

Yes, Thanks a lot @tkhunny , this is actually cross product which they mistakenly typed to be cross multiplication.
But the cross multiplication has still been used, for which the explanation is very much incorrectly placed.

Thanks !