Curvalinear distance bewteen two points on a cylinder (geodesic)

[rww88]

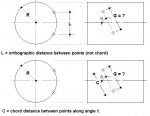
I would like to develop two formulas that would determine the curvalinear distance between two points on a cylinder. The radius R and the angle theta a line between the the two points makes with the cylinder's longitudinal axis are known in each case. In the first formula the orthographic (vertical) distance L between the two points is known. Note: this is not the chord between the two points; it is the distance between the two points along the circumferential axis. In the second formula the chord distance C between the two points along the inclined line in known. In both cases the formulas would result in the geodesic G.

 

[rww88]

Hopefully a better explanation

Two points on the surface of a cylinder lie along a line that is inclined from the longitudinal axis of the cylinder. Suppose that this inclination angle as well as the radius of the cylinder are known. Suppose that the linear distance between lines that coincide with these points and that are parallel to the cylinder's longitudinal axis is also known. If the end of the cylinder is viewed, this linear distance could be represented by a vertical line that is parallel to the vertical centerline of the cylinder. The development of a formula is desired that would calculate the curvalinear distance (geodesic) between the two points along the surface of the cylinder knowing the radius, inclination angle, and linear offset distance between the two points parallel to the vertical centerline.