Hi! i need some help on this question.
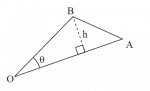
In the triangle below, the lengths of OA and OB are LA and LB respectively.
(i) Determine an expression for the length h and an expression for the area of the triangle in terms of θ, LA and LB only.
(ii) Hence, determine the area given OA = i + j + k and OB = i − 2j .

there is what i got so far.
i) h = LBSinθ
Area = LALBSinθ/2
ii) LA = 3^(1/2), LB = 5^(1/2)
How do i solve for the area if i don't know the height and θ?
In the triangle below, the lengths of OA and OB are LA and LB respectively.
(i) Determine an expression for the length h and an expression for the area of the triangle in terms of θ, LA and LB only.
(ii) Hence, determine the area given OA = i + j + k and OB = i − 2j .
there is what i got so far.
i) h = LBSinθ
Area = LALBSinθ/2
ii) LA = 3^(1/2), LB = 5^(1/2)
How do i solve for the area if i don't know the height and θ?