dirac delta function - 2

[logistic_guy]

Solve the differential equation the hard way by Dirac delta function to obtain Green's function.

\(\displaystyle \frac{d^2y}{dx^2} + k^2y = f(x)\)

\(\displaystyle a < x < b\)

 

[logistic_guy]

[imath]\large g(x,s) =\begin{cases} A\cos kx + B\sin kx & a \leq s < x\\[2ex] C\cos kx + D\sin kx & x < s \leq b\end{cases}[/imath]

 

[logistic_guy]

[imath]\large g(x,s) =\begin{cases} A\cos kx + B\sin kx & a \leq s < x\\[2ex] C\cos kx + D\sin kx & x < s \leq b\end{cases}[/imath]

This should be written as:

[imath]\large g(x,s) =\begin{cases} A\cos ks + B\sin ks & a \leq s < x\\[2ex] C\cos ks + D\sin ks & x < s \leq b\end{cases}[/imath]

 

[logistic_guy]

[imath]\large g(x,s) =\begin{cases} A\cos ks + B\sin ks & a \leq s < x\\[2ex] C\cos ks + D\sin ks & x < s \leq b\end{cases}[/imath]

As I said before, \(\displaystyle A, B, C, \text{and} \ D\) are not constants, but rather functions of \(\displaystyle x\). And the goal is find them to get Green's function.

Four unknowns need \(\displaystyle 4\) equations. We can get two of them from boundary conditions and two from continuity conditions. That is FOUR.

\(\displaystyle A\cos ka + B\sin ka = 0\)
\(\displaystyle C\cos kb + D\sin kb = 0\)
\(\displaystyle A\cos kx + B\sin kx - C\cos kx - D\sin kx = 0\)
\(\displaystyle -kC\sin kx + kD\cos kx + kA\sin kx - kB\cos kx = 1\)

 

[logistic_guy]

We will use a calculator to solve this system. This calculator does not accept functions so we will replace them with letters.

\(\displaystyle F = \cos ka\)
\(\displaystyle G = \sin ka\)
\(\displaystyle H = \cos kb\)
\(\displaystyle L = \sin kb\)
\(\displaystyle Y = \cos kx\)
\(\displaystyle Z = \sin kx\)

 

[logistic_guy]

If I solve this systems of equations, I get:

\(\displaystyle A = \frac{\sin ka\sin k(b-x)}{k\sin k(b - a)}\)

\(\displaystyle B = -\frac{\cos ka\sin k(b-x)}{k\sin k(b - a)}\)

\(\displaystyle C = -\frac{\sin kb\sin k(x-a)}{k\sin k(b - a)}\)

\(\displaystyle D = \frac{\cos kb\sin k(x-a)}{k\sin k(b - a)}\)

 

[logistic_guy]

Our Green function so far:


[imath] \Large g(x,s) =\begin{cases} \left(\frac{\sin ka\sin k(b-x)}{k\sin k(b - a)}\right)\cos ks + \left(-\frac{\cos ka\sin k(b-x)}{k\sin k(b - a)}\right)\sin ks & a \leq s < x\\[3ex] \left(-\frac{\sin kb\sin k(x-a)}{k\sin k(b - a)}\right)\cos ks + \left(\frac{\cos kb\sin k(x-a)}{k\sin k(b - a)}\right)\sin ks & x < s \leq b \end{cases} [/imath]

 

[logistic_guy]

With a little simplification, we get:


[imath] \Large g(x,s) =\begin{cases} \left(\frac{\sin k(b-x)}{k\sin k(b - a)}\right)(\sin ka\cos ks - \cos ka \sin ks) & a \leq s < x\\[3ex] \left(\frac{\sin k(x-a)}{k\sin k(b - a)}\right)(-\sin kb\cos ks + \cos kb\sin ks) & x < s \leq b \end{cases} [/imath]

 

[logistic_guy]

[imath] \Large g(x,s) =\begin{cases} \left(\frac{\sin k(b-x)}{k\sin k(b - a)}\right)(\sin ka\cos ks - \cos ka \sin ks) & a \leq s < x\\[3ex] \left(\frac{\sin k(x-a)}{k\sin k(b - a)}\right)(-\sin kb\cos ks + \cos kb\sin ks) & x < s \leq b \end{cases} [/imath]

We simplify the expression above to get:

[imath] \Large g(x,s) =\begin{cases} \left(\frac{\sin k(b-x)}{k\sin k(b - a)}\right)\sin k(a - s) & a \leq s < x\\[3ex] \left(\frac{\sin k(x-a)}{k\sin k(b - a)}\right)\sin k(s - b) & x < s \leq b \end{cases} [/imath]


Or


[imath] \Large g(x,s) =\begin{cases} -\frac{\sin k(s - a)\sin k(b-x)}{k\sin k(b - a)} & a \leq s < x\\[3ex] -\frac{\sin k(x-a)\sin k(b - s)}{k\sin k(b - a)} & x < s \leq b \end{cases} [/imath]

Which matches the result of this post:

green function

Find Green's function for the following differential equation: \frac{d^2y}{dx^2} + k^2y = f(x) a < x < b Then use it to find the solution of: \frac{d^2y}{dx^2} + 4y = x y(1) = 5 y(5) = 1 1 < x < 5 Solve the differential equation again with your favorite normal method. Does your answer...

www.freemathhelp.com

Which means we have found the Green's function successfully the hard way!

 

[logistic_guy]

I will show what I entered in the calculator and what it gave me back!



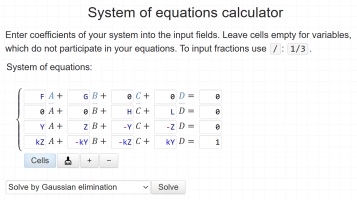
And it gave me this solution:

\(\displaystyle A = \frac{\sin ka\sin k(b-x)}{k\sin k(b - a)}\)

Let us take, for example, \(\displaystyle A\) from the calculator and simplify it to see if it matches the above.

\(\displaystyle A = \frac{-GLY + GHZ}{GHY^2k - FLY^2k + GHZ^2k - FLZ^2k}\)


\(\displaystyle = \frac{G(HZ - LY)}{(GH - FL)kY^2 + (GH - FL)kZ^2}\)


\(\displaystyle = \frac{G(HZ - LY)}{(GH - FL)(kY^2 + kZ^2)}\)


\(\displaystyle = \frac{G(HZ - LY)}{k(GH - FL)(\cos^2 kx + \sin^2 kx)}\)


\(\displaystyle = \frac{G(HZ - LY)}{k(GH - FL)(1)}\)


\(\displaystyle = \frac{G(HZ - LY)}{k(GH - FL)}\)


\(\displaystyle = \frac{\sin ka(\cos kb \sin kx - \sin kb \cos kx)}{k(\sin ka \cos kb - \cos ka\sin kb)}\)


\(\displaystyle = \frac{\sin ka\sin k(x - b)}{k\sin k(a - b)}\)


\(\displaystyle = \frac{\sin ka\sin k(b - x)}{k\sin k(b - a)}\)

Which matches the first result below:

If I solve this systems of equations, I get:

\(\displaystyle A = \frac{\sin ka\sin k(b-x)}{k\sin k(b - a)}\)

\(\displaystyle B = -\frac{\cos ka\sin k(b-x)}{k\sin k(b - a)}\)

\(\displaystyle C = -\frac{\sin kb\sin k(x-a)}{k\sin k(b - a)}\)

\(\displaystyle D = \frac{\cos kb\sin k(x-a)}{k\sin k(b - a)}\)