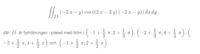Dubbel integral given 4 corners

[AnyHelpIsAppreciated]

Calculate the dubbel integral of (-2x-y)*cos( (2x-2y)*(-2x-y)) dxdy over the area D which is the quadrilateral with corners in (-1+pi/3,2+pi/3),(-2+pi/3m4+pi/3),(-2+pi/2,4+pi/2) and (-1+pi/2,2+pi/2)...

I calculated the equations for the lines between the corners and they are:
y1=x+(2+pi/3)
y2=-x+(2+pi/2)
y3=x+(4+pi/3)
y4=-x+(2+pi/3)

II was wondering what a suitable variable switch might be so that they get constant limits?

 

[AmandasMathHelp]

You might want to check your lines. I got y=x+6, y=x+3, y=-2x+pi, and y=-2x+3pi/2. If you rearrange those so that the ys and xs are on the same side you get.
y-x=6
y-x=3
y+2x=pi
y+2x=3pi/2.

Clearly, now if you do y-x as a new variable and y+2x as a new variable then these bounds of the region turn into constants (the ones above). I don't have a lot of experience in doing a change in variables like this so I probably won't attempt it but I hope that helps!