Exact values

[carebear]

What is the exact value of sin(cos^-1(-3/5))?

How do I do this without a calculator?

 

[Deleted member 4993]

What is the exact value of sin(cos^-1(-3/5))?

How do I do this without a calculator?

Start with:

\(\displaystyle cos(\theta) \ = \ \frac{-3}{5}\)

then

\(\displaystyle sin(\theta)\ = \ ???\)

 

[carebear]

-4/5 or 4/5

 

[Deleted member 4993]

and you have solved your problem.......

 

[carebear]

the answer though is saying that it is just 4/5 and not -4/5.....can you please tell me why? Is it to do with the inverse?

 

[pka]

the answer though is saying that it is just 4/5 and not -4/5.....can you please tell me why? Is it to do with the inverse?

Because \(\displaystyle \arccos\left(\frac{-3}{5}\right)\in II\).
The sine function is positive in \(\displaystyle II\).

 

[carebear]

I understand that sin is positive in Quad 2....why does arccos (-3/5) have to be in Quad 2? I am missing something there.

Thank you

 

[pka]

why does arccos (-3/5) have to be in Quad 2? I am missing something there

You are missing this: \(\displaystyle \left( {\forall x} \right)\left[ { - 1 \leqslant x \leqslant 1\, \Rightarrow \,0 \leqslant \arccos (x) \leqslant \pi } \right]\).

In other words, be mindful of the domain and range of the arccosine function.

 

[mmm4444bot]

I am missing something there.

I think so, but I'm not sure what.

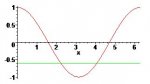
[attachment=0:1sqvu9dd]Cosine.JPG[/attachment:1sqvu9dd]

The red graph is y = cos(x)

The green graph is y = -3/5

We see that two angles whose cosine is -3/5 are 2.2143 radians and 4.0689 radians (both rounded).

In other words:

cos(2.2143) = -3/5

sin(2.2143) = 4/5

cos(4.0689) = -3/5

sin(4.0689) = -4/5

Yet, 4.0689 radians is not in the range of arccos, so the answer is 4/5.