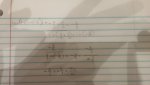So I understand sum/difference formula of sin and cos but im currently stumped by the way this tan difference formula is laid out because Im not sure if I should find the cos/sin of the angles first or just use the formula with the fractions as is. Im on a phone so I apologize for any errors:
Use the information given below to find tan(α-β)
cos(α)=-3/5, with α in quadrant II
sin(b)=−4/5, with β in quadrant III
Give the exact answer, not a decimal approximation.
This is how i worked the problem and the answer I got:
For cos(a) i drew a diagram and put -3 as x and 5 as c since y is unknown i used pythag theorum to find y and then i get tan(a) to use in the tan difference formula
For sin(b) i did the same thing and got tan(b) from the diagram usong pythag theorum.
My tan(a-b) formula looked like this:
Tan((-4/3) - (4/3)) = -4/3 - 4/3 all divided by 1 + (4/3 * -4/3)
I came out with 72/21 but im pretty sure that isnt right. First off none of the solvers i use. To check it agreed with me, one said 1/5, and im just not sure if im doing it correct. Please help..
Use the information given below to find tan(α-β)
cos(α)=-3/5, with α in quadrant II
sin(b)=−4/5, with β in quadrant III
Give the exact answer, not a decimal approximation.
This is how i worked the problem and the answer I got:
For cos(a) i drew a diagram and put -3 as x and 5 as c since y is unknown i used pythag theorum to find y and then i get tan(a) to use in the tan difference formula
For sin(b) i did the same thing and got tan(b) from the diagram usong pythag theorum.
My tan(a-b) formula looked like this:
Tan((-4/3) - (4/3)) = -4/3 - 4/3 all divided by 1 + (4/3 * -4/3)
I came out with 72/21 but im pretty sure that isnt right. First off none of the solvers i use. To check it agreed with me, one said 1/5, and im just not sure if im doing it correct. Please help..