You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
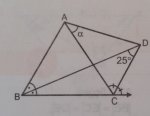
finding angle alpha in quadrilateral ABCD (please see picture)
- Thread starter ketanco
- Start date
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
ketanco, Please clarify what the notation in the diagram means.what is the angle alpha in the attached?
the other angle near alpha at point A should b 50 degrees. but then i can not proceed.
View attachment 10457
For example: it clear that \(\displaystyle \overline{DC}\) bisects \(\displaystyle \angle C\).
BUT do the 'dots' mean that \(\displaystyle \overline{DB}\) bisects \(\displaystyle \angle ABC~?\).
And are you saying that \(\displaystyle \angle BAC\) should measure \(\displaystyle 50^o~?\)
yes DB bisects ABC and therefore BAC must be 50ketanco, Please clarify what the notation in the diagram means.
For example: it clear that \(\displaystyle \overline{DC}\) bisects \(\displaystyle \angle C\).
BUT do the 'dots' mean that \(\displaystyle \overline{DB}\) bisects \(\displaystyle \angle ABC~?\).
And are you saying that \(\displaystyle \angle BAC\) should measure \(\displaystyle 50^o~?\)
I look for alpha
ketanco, Please clarify what the notation in the diagram means.
For example: it clear that \(\displaystyle \overline{DC}\) bisects \(\displaystyle \angle C\).
BUT do the 'dots' mean that \(\displaystyle \overline{DB}\) bisects \(\displaystyle \angle ABC~?\).
And are you saying that \(\displaystyle \angle BAC\) should measure \(\displaystyle 50^o~?\)
is abc an equilateral triangle?
is ab parralel to cd?
how did you get 500 ?
is abc an equilateral triangle?
is ab parralel to cd?
how did you get 500 ?
no and no
well you can forget about 50 if you want and solve like this... i saw a formula for that ... that is all...
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,854
what is the angle alpha in the attached?
the other angle near alpha at point A should b 50 degrees. but then i can not proceed.
View attachment 10457
I do obtain BAC = 50, by working only with angles (starting by calling ABD "x" and expressing other angles in terms of that. I suspect that finding alpha may require a little trigonometry. Are you able to use that?
What is the context of this problem? And where did you get your 50? Any information you can give can help us know what kind of solution to try, and what kind of hints will be useful.
I do obtain BAC = 50, by working only with angles (starting by calling ABD "x" and expressing other angles in terms of that. I suspect that finding alpha may require a little trigonometry. Are you able to use that?
What is the context of this problem? And where did you get your 50? Any information you can give can help us know what kind of solution to try, and what kind of hints will be useful.
I got 50 from a formula relating internal and external angle bisectors
so yes as you also stated, 50 is right. i just cannot figure out alpha
I do not think trigonometry is needed, as this was one of a test question in a chapter only about triangle angles without any trigonometry. solution should be simpler - unless question is wrong... but i cannot verify it now but the question should be ok.... it is very little possibility that question is wrong
Bob Brown MSEE
Full Member
- Joined
- Oct 25, 2012
- Messages
- 598
Choose a simple example.
1) There is no single answer, (function of an unknown variable)
2) The answer is independent of which legal configuration you choose.
The problem seems to imply possibility number 2.
It turns out that possibility number 2 is correct, but difficult to prove.
If we assume possibility number 2 is implied then we can pick a convenient one!
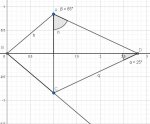
The answer is obviously 65 degrees.
There are an infinite number of dissimilar configurations that are consistent with the given problem description. Therefore there are 2 possibilities.what is the angle alpha in the attached?
1) There is no single answer, (function of an unknown variable)
2) The answer is independent of which legal configuration you choose.
The problem seems to imply possibility number 2.
It turns out that possibility number 2 is correct, but difficult to prove.
If we assume possibility number 2 is implied then we can pick a convenient one!

The answer is obviously 65 degrees.
Last edited:
i got the solution.....
point D is equidistant from the three lines that form ABC trinagle... why? because a point on angle bisector is equidistant from the two lines....
so it makes point D a circle center to those 3 lines....
then alpha = (180 - angle BAC) / 2, if you look at that circle
and yes 65 is correct
point D is equidistant from the three lines that form ABC trinagle... why? because a point on angle bisector is equidistant from the two lines....
so it makes point D a circle center to those 3 lines....
then alpha = (180 - angle BAC) / 2, if you look at that circle
and yes 65 is correct
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,854
i got the solution.....
point D is equidistant from the three lines that form ABC trinagle... why? because a point on angle bisector is equidistant from the two lines....
so it makes point D a circle center to those 3 lines....
then alpha = (180 - angle BAC) / 2, if you look at that circle
and yes 65 is correct
I found a related method, observing that the circumcenter of ABC lies on the circumcircle of ACD. Yours is better.