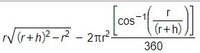I've been working on this problem for several days and cannot come up with a solution.
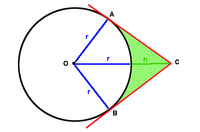
Find the area of the shaded (light green) area as a function of r (radius of the circle) and h (distance to C from the circumference of the circle). h is the extension of a radius. Lines AC and BC are tangent to the circle.
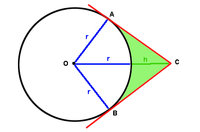
Find the area of the shaded (light green) area as a function of r (radius of the circle) and h (distance to C from the circumference of the circle). h is the extension of a radius. Lines AC and BC are tangent to the circle.