Problem
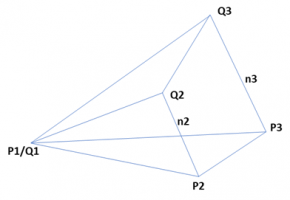
See attached drawing.
I need to find the normal unit vector of the plane defined by the points Q1, Q2 and Q3
I have 3 known points P1 (=Q1), P2 and P3.
n2 and n3 are normal to the plane defined by Q1, Q2 and Q3
The lengths of n2 and n3 are known.
There should be 2 solutions as the Q-plane can be at the other side of the P- triangle as well
How to solve this?
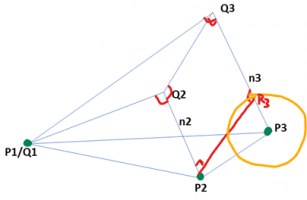
See attached drawing.
I need to find the normal unit vector of the plane defined by the points Q1, Q2 and Q3
I have 3 known points P1 (=Q1), P2 and P3.
n2 and n3 are normal to the plane defined by Q1, Q2 and Q3
The lengths of n2 and n3 are known.
There should be 2 solutions as the Q-plane can be at the other side of the P- triangle as well
How to solve this?