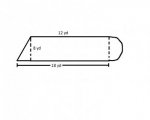
Find the area and perimeter of the following figure. Your final answer may include the pi.
Here is what I had:
First I needed to find the missing measurements for the triangle so I subtracted 12 from 18 to give us our base of the triangle (6yd). Next I used the Pythagorean Theorem to find the hypotenuse of the triangle.
8^2 + 6^2 = c^2
64 + 36 = c^2
100 = c^2
10 = c
Now I had the measurements for the triangle. Next was to find the radius of the semicircle. Since the measurement of 8yds was going to be the diameter. I divided 8 by 2 to find our radius of 4. We have all our missing measurements to solve now.
12 x 8 = 96yd <--area of rectangle
2(12 + 8) = 40yd <--perimeter of rectangle
1/2 x 6 x 8 = 24yd <--area of triangle
10 + 8 + 6 = 24yd <-- perimeter of triangle
pi x 4^2 = 16piyd^2 <--area of semicircle
pi x 4 = 4pi <-- perimeter of semicircle
We take all our measurements and add them together for the area of the figure:
96 + 24 + 16pi = 136piyd2 is the total area of the figure
For the total perimeter I believe it would be a little different than adding them all together because we do not want to include the lines inside the figure. So we would just add the exterior measurements together.
For the total perimeter I believe it would be a little different than adding them all together because we do not want to include the lines inside the figure. So we would just add the exterior measurements together.
10 = 18 = 12 = 4pi = 44piyd^2 total perimeter of the figure
I have total area as 136piyd^2 and total perimeter of 44piyd^2.
Am I totally off on this? I thought it would be asiest to break the shape down and go from there.
Here is what I had:
First I needed to find the missing measurements for the triangle so I subtracted 12 from 18 to give us our base of the triangle (6yd). Next I used the Pythagorean Theorem to find the hypotenuse of the triangle.
8^2 + 6^2 = c^2
64 + 36 = c^2
100 = c^2
10 = c
Now I had the measurements for the triangle. Next was to find the radius of the semicircle. Since the measurement of 8yds was going to be the diameter. I divided 8 by 2 to find our radius of 4. We have all our missing measurements to solve now.
12 x 8 = 96yd <--area of rectangle
2(12 + 8) = 40yd <--perimeter of rectangle
1/2 x 6 x 8 = 24yd <--area of triangle
10 + 8 + 6 = 24yd <-- perimeter of triangle
pi x 4^2 = 16piyd^2 <--area of semicircle
pi x 4 = 4pi <-- perimeter of semicircle
We take all our measurements and add them together for the area of the figure:
96 + 24 + 16pi = 136piyd2 is the total area of the figure
For the total perimeter I believe it would be a little different than adding them all together because we do not want to include the lines inside the figure. So we would just add the exterior measurements together.
For the total perimeter I believe it would be a little different than adding them all together because we do not want to include the lines inside the figure. So we would just add the exterior measurements together.
10 = 18 = 12 = 4pi = 44piyd^2 total perimeter of the figure
I have total area as 136piyd^2 and total perimeter of 44piyd^2.
Am I totally off on this? I thought it would be asiest to break the shape down and go from there.