jonnburton
Junior Member
- Joined
- Dec 16, 2012
- Messages
- 155
Hi,
There is a worked example in the book I am using which I don't quite understand. Can anybody tell me how the following is the case?
The working comes from the following free body diagram:
The boom is used to support a 75lb flower pot. Determine the tension in the wires AB and AC.
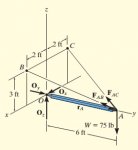
The first step is to get the unit vector for the lines AB and AC, which is fine.
\(\displaystyle F_{AB} = F_{AB}(\frac{(2i - 6j +3k)ft}{(2ft)^2+(-6ft)^2 + (3ft)^2})\)
\(\displaystyle F_{AB} = \frac{2}{7}F_{AB}i-\frac{6}{7}F_{AB}j+\frac{3}{7}F_{AB}k\)
And, likewise \(\displaystyle F_{AC} =\frac{-2}{7}F_{AC}i -\frac{6}{7}F_{AC}j +\frac{3}{7}F_{AC}k\)
The next step is to eliminate the force reaction at O by writing the moment equation of equilibrium about O.
\(\displaystyle \sum M_o = 0\)
\(\displaystyle r_A * (F_{AB} + F_{AC} + W) = 0\)
This is the part I don't see. It is clear that the perpendicular distance from the weight force is \(\displaystyle r_A\), but \(\displaystyle r_A \) is not the perpendicular distance to point O for either \(\displaystyle F_{AB}\) or \(\displaystyle F_{AC}\)
I know I must be forgetting something I should have learned earlier here but I can't see how it can be said the moment of \(\displaystyle F_{AB}\) and \(\displaystyle F_{AC}\) about point O is obtained by multiplying these forces by something that is not the perpendicular distance. Can anyone tell me what I am missing?
There is a worked example in the book I am using which I don't quite understand. Can anybody tell me how the following is the case?
The working comes from the following free body diagram:
The boom is used to support a 75lb flower pot. Determine the tension in the wires AB and AC.

The first step is to get the unit vector for the lines AB and AC, which is fine.
\(\displaystyle F_{AB} = F_{AB}(\frac{(2i - 6j +3k)ft}{(2ft)^2+(-6ft)^2 + (3ft)^2})\)
\(\displaystyle F_{AB} = \frac{2}{7}F_{AB}i-\frac{6}{7}F_{AB}j+\frac{3}{7}F_{AB}k\)
And, likewise \(\displaystyle F_{AC} =\frac{-2}{7}F_{AC}i -\frac{6}{7}F_{AC}j +\frac{3}{7}F_{AC}k\)
The next step is to eliminate the force reaction at O by writing the moment equation of equilibrium about O.
\(\displaystyle \sum M_o = 0\)
\(\displaystyle r_A * (F_{AB} + F_{AC} + W) = 0\)
This is the part I don't see. It is clear that the perpendicular distance from the weight force is \(\displaystyle r_A\), but \(\displaystyle r_A \) is not the perpendicular distance to point O for either \(\displaystyle F_{AB}\) or \(\displaystyle F_{AC}\)
I know I must be forgetting something I should have learned earlier here but I can't see how it can be said the moment of \(\displaystyle F_{AB}\) and \(\displaystyle F_{AC}\) about point O is obtained by multiplying these forces by something that is not the perpendicular distance. Can anyone tell me what I am missing?
