Everything4pageants
New member
- Joined
- Jan 5, 2011
- Messages
- 4
1. find all pairs of prime numbers whose sum equals 999
2. A basketball player attempts a free throw. If she is successful she can attempt a second. If p is the probability of a successful throw and if her probability of making 0 points is equal to that of making 2 points what is P? Round to the nearest thousandth.
3. Total # of interior angels in two regular polygons is 17. and the total number of diagonals is 63. How many sides does each regular polygon have?
4.
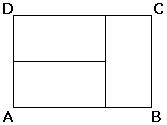
3 congruent rectangles are placed to form a larger rectangle as shown with an area of 1350cm squared. Find the area of a square that has the same perimeter of the larger rectangle.
Help I have two days to figure these out. I really need the EC.
2. A basketball player attempts a free throw. If she is successful she can attempt a second. If p is the probability of a successful throw and if her probability of making 0 points is equal to that of making 2 points what is P? Round to the nearest thousandth.
3. Total # of interior angels in two regular polygons is 17. and the total number of diagonals is 63. How many sides does each regular polygon have?
4.

3 congruent rectangles are placed to form a larger rectangle as shown with an area of 1350cm squared. Find the area of a square that has the same perimeter of the larger rectangle.
Help I have two days to figure these out. I really need the EC.
