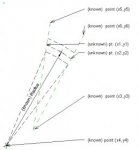
Exactly what do you mean by "know the locations of the green lines". Do you know the angles they make with, say, a a horizontal line and the distance from points \(\displaystyle (x_1, y_1)\) and \(\displaystyle (x_2, y_2)\) to \(\displaystyle (x_3, y_2)\)?
If the line segment from \(\displaystyle (x_3, y_3)\) to \(\displaystyle (x_1, y_1)\) has length \(\displaystyle r_1\) and makes angle \(\displaystyle \theta_1\) with the horizontal, then \(\displaystyle x_1= x_3+ r_1 cos(\theta_1)\) and \(\displaystyle y_1= y_3+ r_1 sin(\theta_1)\). Similarly, if the line segment from \(\displaystyle (x_3, y_3)\) to \(\displaystyle (x_2, y_2)\) has length \(\displaystyle r_2\) and makes angle \(\displaystyle theta_2\) with the horizontal, then \(\displaystyle x_2= x_3+ r_2 cos(\theta_2)\) and \(\displaystyle y_2= y_3+ r_2 sin(\theta_2)\).
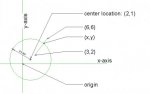
Now, we want to find \(\displaystyle (x_4, y_4)\), the center of a circle of radius r, passing through \(\displaystyle (x_1, y_1)\) and \(\displaystyle (x_2, y_2)\). The perpendicular bisector of a chord of a circle will pass through the center of the circle so first find the midpoint of the segment from \(\displaystyle (x_1, y_1)\) to \(\displaystyle (x_2, y_2)\). That is \(\displaystyle \left(\frac{x_1+ x_2}{2}, \frac{y_1+ y_2}{2}\right)\). The line segment between those two points has slope \(\displaystyle \frac{y_2- y_1}{x_2- x_1}\) so the perpendicular bisector has slope \(\displaystyle \frac{x_2- x_1}{y_1- y_2}\). With that information, you can write the equation of the perpendicular bisector. Finally, write the equation of the circle with center at \(\displaystyle \left(\frac{x_1+ x_2}{2}, \frac{y_1+ y_2}{2}\right)\). That circle will intersect the perpendicular bisector in two points one of them is your \(\displaystyle (x_4, y_4)\).