Mei_Mienzi
New member
- Joined
- Jul 26, 2016
- Messages
- 1
Hello:
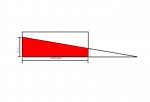
I am not sure if my question belongs on this forum or not, but either way I am hoping that I can get some help. I have attached a picture of my problem, hoping that it will help (I'm a visual person). You will note a rectangle representing a piece of wood that needs to be cut as noted in red. Adjacent to the rectangle is a right triangle for which the base and hypotenuse are unknown. I know that by extending the base of the rectangle and the line above it (not sure what you call it) that the two lines will meet, forming the right triangle. However, I do not know how far either of those line have to be extended to the point of intersection. If I knew that I could calculate the desired angle of cut. I would think that this would be a common problem for a carpenter, which I am not, and therefore not all that hard to figure out (though I haven't a clue). Can someone help me? Thanks.
I am not sure if my question belongs on this forum or not, but either way I am hoping that I can get some help. I have attached a picture of my problem, hoping that it will help (I'm a visual person). You will note a rectangle representing a piece of wood that needs to be cut as noted in red. Adjacent to the rectangle is a right triangle for which the base and hypotenuse are unknown. I know that by extending the base of the rectangle and the line above it (not sure what you call it) that the two lines will meet, forming the right triangle. However, I do not know how far either of those line have to be extended to the point of intersection. If I knew that I could calculate the desired angle of cut. I would think that this would be a common problem for a carpenter, which I am not, and therefore not all that hard to figure out (though I haven't a clue). Can someone help me? Thanks.