markosheehan
New member
- Joined
- May 12, 2016
- Messages
- 31
given the differential equation dy/dx=y cosx
find the general solution given that y=2 when x= π /6
i cant solve this
i tried integration
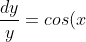dx) but then i get ln(2)=sinx+c and then when i put in 2 for y and π /6 for x i get ln(2)=1/2 + c and this is not the answer the answer is y=2e^sinx-0.5
but then i get ln(2)=sinx+c and then when i put in 2 for y and π /6 for x i get ln(2)=1/2 + c and this is not the answer the answer is y=2e^sinx-0.5
find the general solution given that y=2 when x= π /6
i cant solve this
i tried integration
