GRE Trig Question

[ash9231]

I cant understand their explanation. And can anyone refresh my memory about what we can infer about similar triangles. please go to the link and see the image.



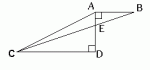
In the figure above AD = 4, AB = 3 and CD = 9. What is the area of triangle AEC ? A. 18 B. 13.5 C. 9 D. 4.5 E. 3 Correct Answer: D Explanation: If we take AE as the base of triangle AEC, then the height is CD. The height of the triangle is therefore, 9 (given). To find the base we need to see that triangles AEB and CDE are similar. The ratio AB: CD, is therefore equal to the ratio AE: ED. The given information shows that the ratio is 3:9, or 1:3. Now dividing AD (4) in this ratio gives us AE as 1. The area of AEC = ½ base x height =1/2 x 9 = 4.5

(the figure is question 10 at this link address http://www.majortests.com/gre/problem_solving_expl.php?exp=50313031243130243135)

 

[HallsofIvy]

Similar triangles are triangles having the same angles but not necessarily the same length sides. It can then be shown that the lengths of the sides are in the same ratios. That is, if triangle ABC is similar to triangle XYZ (the angle at vertex A the same as the angle at vertex X, etc.) then \(\displaystyle \frac{AB}{XY}= \frac{BC}{YZ}= \frac{AC}{XZ}\).