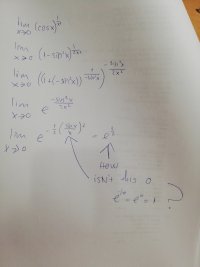Hooow

Have you not learned that [math]\lim_{x\to0}\frac{\sin x}{x}=1 ?[/math]
This is a theorem that we commonly memorize because it is used often. If you just substituted 0 for x, you would get 0/0, not 0; that means you need to take a different approach.
 
You've switched the sign in the end, but otherwise it looks good to me. But I don't get your question, i.e. "How isn't it 0".
 
Many students think that sinx/x=1 (not 0) but they are wrong! Think about the fact that the numerator, sinx, is always between -1 and 1 inclusive while the denominator can be say 10000. A number between -1 and 1 when divided by 10,000 is not 1 (or 0-usually). What the statement should be, as Dr Peterson pointed out, is that as x approaches 0, sinx/x approaches 1
 
You must log in or register to reply here.
Top