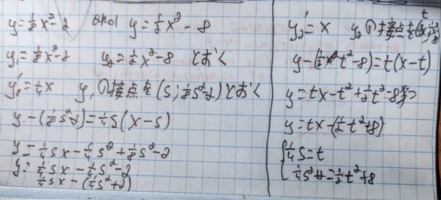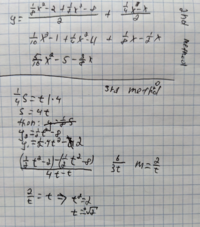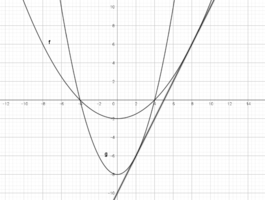
How do I find tangent line common to y = (1/8)x^2 - 2 and y = (1/2)x^2 - 8?
- Thread starter Felix_GG
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
Please show one of your attempts, so we can see how close you are to a correct solution, and where we might correct you, if necessary.
Start by NAMING things that may be relevant.
Let (u, v) identify the the point of tangency for [imath]x^2/8 \ - 2[/imath].
Let w = the slope at (u, v).
Let (p, q) identify the the point of tangency for [imath]x^2/2 \ - 8[/imath].
Let r = the slope at (p, q).
We are given that u > 0 and p > 0.
Let the line coincident with both tangent lines be described by [imath]y = a + bx.[/imath]
How many unknowns do you have?
So how many equations do you need to find a solution set for that many unknowns?
Four are mechanical. Develop equations v = what, q = what, w = what, r = what.
Now you must think. How many more independent equations do you need? What relevant information have you not used yet?
Hint:
Let (u, v) identify the the point of tangency for [imath]x^2/8 \ - 2[/imath].
Let w = the slope at (u, v).
Let (p, q) identify the the point of tangency for [imath]x^2/2 \ - 8[/imath].
Let r = the slope at (p, q).
We are given that u > 0 and p > 0.
Let the line coincident with both tangent lines be described by [imath]y = a + bx.[/imath]
How many unknowns do you have?
So how many equations do you need to find a solution set for that many unknowns?
Four are mechanical. Develop equations v = what, q = what, w = what, r = what.
Now you must think. How many more independent equations do you need? What relevant information have you not used yet?
Hint:
b = r = w. Why?
Oh, yeah, right. I forgot about it. There is a little bit of Japanese here, if something is unclear lt me know.
Wow, i don't know why, but when i tried do everything for the second time i got the answer correct. I did look for mistakes in previous writing, but everything correct in that writing too. Maybe i just overlooked something, my clumsiness. Anyway thanks for help and for the reply.
Good that you got there... There is an alternative method without using calculus you might be interested in. This involves using the discriminant.
So start off by trying to solve points of intersection of (1/8)x^2-2= mx+c and (1/2)x^2-8=mx+c.
This leads to two quadratic equations in m and c.
For tangency we need repeated roots, so b^2-4ac=0.
And see if you can go from there...
So start off by trying to solve points of intersection of (1/8)x^2-2= mx+c and (1/2)x^2-8=mx+c.
This leads to two quadratic equations in m and c.
For tangency we need repeated roots, so b^2-4ac=0.
And see if you can go from there...
