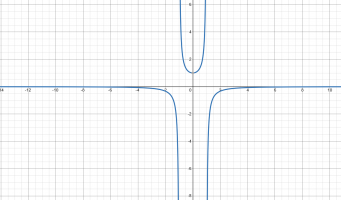
After doing all of this I thought 'well, here's the absolute min' but then I checked with a function plotter and the function looks like this, meaning there is no absolute min/max:
Is there a way to tell by just looking at the little scheme I drew on the right, without going through all the steps to draw a graph?
Before seeing the graph I knew that this is a function of the kind x^-2 and is therefore not continuous. How does this help?
