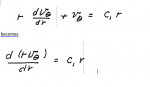shreddinglicks
Junior Member
- Joined
- Apr 16, 2016
- Messages
- 76
This is part of a derivation involving the Navier-Stokes equation for fluid mechanics.
How does this:
. . . . .\(\displaystyle r\, \dfrac{dv_{\theta}}{dr}\, +\, v_{\theta}\, =\, c_1\, r\)
become this:
. . . . .\(\displaystyle \dfrac{d\, (r v_{\theta})}{dr}\, =\, c_1\, r\)
How do I manipulate the problem?
How does this:
. . . . .\(\displaystyle r\, \dfrac{dv_{\theta}}{dr}\, +\, v_{\theta}\, =\, c_1\, r\)
become this:
. . . . .\(\displaystyle \dfrac{d\, (r v_{\theta})}{dr}\, =\, c_1\, r\)
How do I manipulate the problem?
Attachments
Last edited by a moderator: