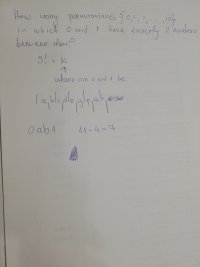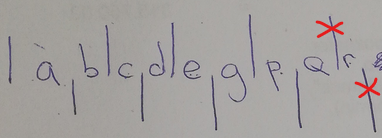You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How many permutations
- Thread starter Loki123
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
I think you have a good idea to start; but I can't be sure, because you haven't told us what you are thinking in words. Once you tell us your thinking, we should be able to help you with the next step.Any advice? I don't know how to do this View attachment 32597
It looks like you are arranging the other 9 numbers, and then thinking about how many places the 0 and 1 can be inserted. But what does 11-4=7 have to do with your thinking? This step should not be hard, once you think clearly about it. (You could just count in your picture.)
i would assume 9! * 10 but it's 9! * 16, which i don't get how they got. 11-4=7 is just an idea that i discardedI think you have a good idea to start; but I can't be sure, because you haven't told us what you are thinking in words. Once you tell us your thinking, we should be able to help you with the next step.
It looks like you are arranging the other 9 numbers, and then thinking about how many places the 0 and 1 can be inserted. But what does 11-4=7 have to do with your thinking? This step should not be hard, once you think clearly about it. (You could just count in your picture.)
blamocur
Elite Member
- Joined
- Oct 30, 2021
- Messages
- 3,222
Can you tell us why '* 10' ?i would assume 9! * 10 but it's 9! * 16, which i don't get how they got. 11-4=7 is just an idea that i discarded
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
[imath]\dbinom{9}{2}=36[/imath] ways to select exactly two other numbers to be between [imath]0~\&~1[/imath].
Lets build a block of those four numbers. That block looks like [imath]\boxed{0XY1}\text{ or }\boxed{1XY0}[/imath]
How many such blocks are there?
Each block can be arranged with the other seven in [imath]8![/imath] ways.
What is the answer?
Lets build a block of those four numbers. That block looks like [imath]\boxed{0XY1}\text{ or }\boxed{1XY0}[/imath]
How many such blocks are there?
Each block can be arranged with the other seven in [imath]8![/imath] ways.
What is the answer?
9! * 16[imath]\dbinom{9}{2}=36[/imath] ways to select exactly two other numbers to be between [imath]0~\&~1[/imath].
Lets build a block of those four numbers. That block looks like [imath]\boxed{0XY1}\text{ or }\boxed{1XY0}[/imath]
How many such blocks are there?
Each block can be arranged with the other seven in [imath]8![/imath] ways.
What is the answer?
i put lines where i think the four 1aa0 could go. 10 places in totalCan you tell us why '* 10' ?
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Why do you say ten places? there are eleven members in [imath]\{0,1,2,3,4,5,6, 7, 8, 9,10\}[/imath]i put lines where i think the four 1aa0 could go. 10 places in total
I get [imath]144[/imath] passible blocks: [imath]\boxed{0XY1}[/imath] The X can have nine values, the Y can have eight.
The block [imath]\boxed{0691}[/imath] can be arranged in four ways: [imath]\boxed{0691}\boxed{1960}\boxed{0961}\boxed{1690}[/imath]
How do we put these together?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,850
If you mean the left end of "1aa0" (or "0aa1") can go, the rightmost 2 don't work.i put lines where i think the four 1aa0 could go. 10 places in total
Or think of it as going in one of these 8 places:
So there are 8 places, and 2 orders, for a total of 9!*8*2.
Got it!! ThanksIf you mean the left end of "1aa0" (or "0aa1") can go, the rightmost 2 don't work.
Or think of it as going in one of these 8 places:
So there are 8 places, and 2 orders, for a total of 9!*8*2.