You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
how the height of a sphere affects the radius
- Thread starter LordExile
- Start date
I am trying to figure out how the radius of my dome will be affected by the height of the dome all while keeping the same surface area.
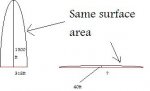
The original dome will have a height of 1500 feet tall with a radius of 318 feet.
The new dome I want to create has 40 feet tall but have the same surface area as the original dome.
The original dome will have a height of 1500 feet tall with a radius of 318 feet.
The new dome I want to create has 40 feet tall but have the same surface area as the original dome.
D
Deleted member 4993
Guest
So the old dome looks like a huge sphere - with a little part of the bottom sectioned off. The bottom section - which is a circle - has a radius of 318 ft. Is that correct?The original dome is 1500 feet tall, and has a radius of 318 feet. The new dome is going to be 40 feet tall, I would like to know in order for it to have the same surface area what the new radius would become?
Diagram of the domes
Sorry for taking so long to post, I was on vacation.

So as you can see the dome of the first one is 1500 feet high, with a radius of 318 feet, the new dome is 40 feet high, but I need the new radius. Both domes need to retain the same surface area.
Sorry for taking so long to post, I was on vacation.
So as you can see the dome of the first one is 1500 feet high, with a radius of 318 feet, the new dome is 40 feet high, but I need the new radius. Both domes need to retain the same surface area.
Attachments
- Joined
- Feb 4, 2004
- Messages
- 16,582
What are the constraints? For instance, is the cross-section of the original dome a parabolic curve? Or some other shape? (This is of course necessary in order to determine the original area.) What is the shape of the new dome, in cross-section?Sorry for taking so long to post, I was on vacation.

So as you can see the dome of the first one is 1500 feet high, with a radius of 318 feet, the new dome is 40 feet high, but I need the new radius. Both domes need to retain the same surface area.
What formulas, methods, rules, etc, have they given you in your class for this project? What have you tried? How far have you gotten? Where are you stuck?
Please be complete. Thank you!
Two domes
Alright so the original dome has a height of 1500 feet, a diameter of 636 feet, a surface area of 2398764 feet, a volume of 317689333.
The new dome has a height of 40 feet, a diameter of X, a surface area of 2398764 feet.
Hense trying to find the diameter of X so that I can calculate the new floor area that the dome covers.
Alright so the original dome has a height of 1500 feet, a diameter of 636 feet, a surface area of 2398764 feet, a volume of 317689333.
The new dome has a height of 40 feet, a diameter of X, a surface area of 2398764 feet.
Hense trying to find the diameter of X so that I can calculate the new floor area that the dome covers.
- Joined
- Feb 4, 2004
- Messages
- 16,582
How did you obtain the surface-area and volume values? What is the cross-section function of the original "spheres"?Alright so the original dome has a height of 1500 feet, a diameter of 636 feet, a surface area of 2398764 feet, a volume of 317689333.
What is to be the cross-sectional function of the new "sphere"? What are the constraints?The new dome has a height of 40 feet, a diameter of X, a surface area of 2398764 feet.
Hence trying to find the diameter of X so that I can calculate the new floor area that the dome covers.
Please be complete. Thank you!
- Joined
- Feb 4, 2004
- Messages
- 16,582
So, use the formulas they use, and work backwards to get the values you want.Unfortunately that is about as precise as I can be, I used the dome calculator from above to get the volume and surface area.
Harry_the_cat
Elite Member
- Joined
- Mar 16, 2016
- Messages
- 3,784
So, use the formulas they use, and work backwards to get the values you want.
What do you mean by a "dome"? Can you define that as you understand it? It'll help us at this end.