These three formulas are all I have been given. Is there any way to use them to solve this?
View attachment 24839
Formulas, unfortunately, mean nothing if their parts are not defined. I hope you were taught what these formulas mean!
The first formula is the
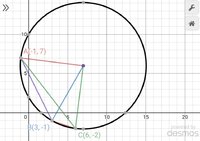
distance formula, giving the distance d between points \((x_1,y_1)\) and \((x_2, y_2)\). That will be useful to find the length of the radius.
The second set of formulas identify a point \((x,y)\) that divides the line segment from \((x_1,y_1)\) to \((x_2, y_2)\) in the proportion \(\lambda:1\). The special case where \(\lambda=1\) is the
midpoint formula, which is useful for finding the perpendicular bisector.
The third formula gives the
area of the triangle with the given coordinates. You could use it if you also knew the second formula in the link I provided, which relates circumradius R to the area and the side lengths a, b, c. But that isn't a formula I myself know without looking it up.
I suggest using the method I showed, which involves finding the equations of two perpendicular bisectors, as you appear to have the required knowledge for that.