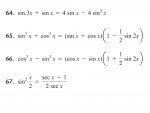Since I am learning by myself and I have no talent, it was inevitable that I would come to such a roadblock. I've completed every problem in the book except for these latest ones...
Please help me with them!!!! But also teach me how to think when verifying these identities! I feel like all my dreams of becoming successful at anything is quickly being deflated. If I can't even do high school math, how can I survive college?
well I've tried and failed to verify all 4 of these... Please teach me how to verify them! Thank you!
Please help me with them!!!! But also teach me how to think when verifying these identities! I feel like all my dreams of becoming successful at anything is quickly being deflated. If I can't even do high school math, how can I survive college?
well I've tried and failed to verify all 4 of these... Please teach me how to verify them! Thank you!