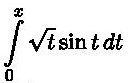Hi! I need to calculate integral numerically using rectangle rule, trapezoidal rule and Simpson's rule. (for the points x = 0.2; 0.3; 0.4; 0.6; 0.9; 1.0).
Could someone explain it to make how to do it at least for 0.2? The rest I would try on my own. I've been reading about it and still have no idea...
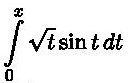
Could someone explain it to make how to do it at least for 0.2? The rest I would try on my own. I've been reading about it and still have no idea...