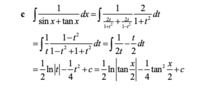You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Integration Q
- Thread starter Sonal7
- Start date
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
What trick do you think you need? It's a couple of basic integrals:I will try thank you. I got it now as you just split up the terms on the top and then cancel the t in one of the new terms.
I now need a trick for the integral. I think there is.
[math]\int \dfrac{1 - t^2}{2t} ~ dt = \int \dfrac{1}{2t} ~ dt - \int \dfrac{t}{2} ~ dt[/math]
[math]\int \dfrac{1}{t} ~ dt = ln|t| + C[/math]
[math]\int t ~ dt = \dfrac{1}{2} t^2 + C[/math]
-Dan
Yes I got that. I don't understand how you get the integral as I am getting ans in decimals if you use the calculator but I think its a whole number. The calculator is not smart you see. I have an idea I will to sub in tan 0.5 and tan 0.25 but I cant figure that out.
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
[math]t = tan \left ( \dfrac{1}{2} x \right )[/math]Thank you very much Dan, atleast I got the main part right. I am just thinking of what they are getting at with the limits of tan .5 and tan 0.25.I slept over it and its not come to me yet.
So, for example, if we have x = 1 then t = tan(1/2) = tan(0.5), so the upper limit on the t integration would be tan(0.5).
-Dan