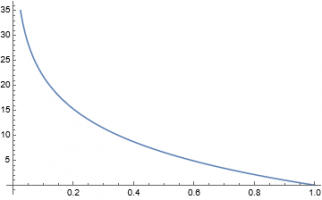
I have a formula y=log(x)/log(0.9), and the graph of it looks like this:
I wish to find the intersection of this curve and a tangent line that appears like so in this rough sketch
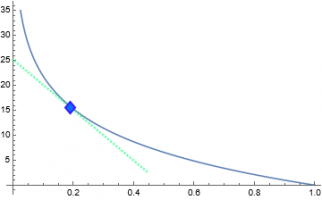
But of course the scales of the axes are quite different, so it's not actually a line with a slope of -1, it just sort of looks that way in this image.
How can I:
1. Figure out what that slope actually is
2. Figure out the coordinates of the intersection?

I wish to find the intersection of this curve and a tangent line that appears like so in this rough sketch

But of course the scales of the axes are quite different, so it's not actually a line with a slope of -1, it just sort of looks that way in this image.
How can I:
1. Figure out what that slope actually is
2. Figure out the coordinates of the intersection?
