drivera001
New member
- Joined
- May 10, 2017
- Messages
- 2
Inverse Laplace Transforms: ay"+by′+cy=0, y(0)=0, y′(0)=0; Y(s) = Theta(s)*F(s)
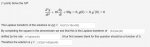
1. Consider the initial value problem for \(\displaystyle 0\, <\, t\, <\, \infty.\)
. . . . .\(\displaystyle a\, y"\, +\, b\, y'\, +\, cy\, =\, 0\). . .\(\displaystyle y(0)\, =\, 0\). . .\(\displaystyle y'(0)\, =\, 0\)
...where a, b, c are constants and f (t ) is a known function. We can view this problem as defining a linear system, where f (t ) is the known input and the corresponding solution y (t ) is the output. Laplace transforms of the input and output functions satisfy the multiplicative relation:
. . . . .\(\displaystyle Y(s)\, =\, \Theta(s)\, F(s)\)
...where \(\displaystyle \Theta(s)\, =\, \dfrac{1}{as^2\, +\, bs\, +\, c}\) is the system transfer function.
Suppose an input f (t ) = 8t, when applied to the linear system above, produces the output:
. . . . .\(\displaystyle y(t)\, =\, 5\, (e^{-3t}\, -\, 1)\, +\, t\, (e^{-3t}\, +\, 14),\, t\, \geq\, 0\)
a. Find \(\displaystyle Y(s)\, =\, \mathcal{L}\{y(t)\}\) and \(\displaystyle F(s)\,=\, \mathcal{L}\{f(t)\}\).
b. Use your answer to part (a) to find the system transfer function, \(\displaystyle \Theta(s).\)
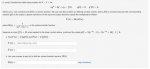
2. Solve the IVP
. . . . .\(\displaystyle \dfrac{d^2 y}{dt^2}\, +\, 16\, \dfrac{dy}{dt}\, +\, 80y\, =\, 0,\, y(0)\, =\, 0,\, y'(0)\, =\, 6\)
c. The Laplace transform of the solutions is:
d. By completing the square in the denominator, we see that this is the Laplace transform of:
e. ...shifted by the rule:
f. Therefore, the solution is y=:
For the second question, i got Y(s) equals (39s+126)/(s^2(s+3)^2) but it says its wrong. The first one i got the answers except i dont know what rule they are referring too... Any help would be greatly appreciated.
1. Consider the initial value problem for \(\displaystyle 0\, <\, t\, <\, \infty.\)
. . . . .\(\displaystyle a\, y"\, +\, b\, y'\, +\, cy\, =\, 0\). . .\(\displaystyle y(0)\, =\, 0\). . .\(\displaystyle y'(0)\, =\, 0\)
...where a, b, c are constants and f (t ) is a known function. We can view this problem as defining a linear system, where f (t ) is the known input and the corresponding solution y (t ) is the output. Laplace transforms of the input and output functions satisfy the multiplicative relation:
. . . . .\(\displaystyle Y(s)\, =\, \Theta(s)\, F(s)\)
...where \(\displaystyle \Theta(s)\, =\, \dfrac{1}{as^2\, +\, bs\, +\, c}\) is the system transfer function.
Suppose an input f (t ) = 8t, when applied to the linear system above, produces the output:
. . . . .\(\displaystyle y(t)\, =\, 5\, (e^{-3t}\, -\, 1)\, +\, t\, (e^{-3t}\, +\, 14),\, t\, \geq\, 0\)
a. Find \(\displaystyle Y(s)\, =\, \mathcal{L}\{y(t)\}\) and \(\displaystyle F(s)\,=\, \mathcal{L}\{f(t)\}\).
b. Use your answer to part (a) to find the system transfer function, \(\displaystyle \Theta(s).\)
2. Solve the IVP
. . . . .\(\displaystyle \dfrac{d^2 y}{dt^2}\, +\, 16\, \dfrac{dy}{dt}\, +\, 80y\, =\, 0,\, y(0)\, =\, 0,\, y'(0)\, =\, 6\)
c. The Laplace transform of the solutions is:
d. By completing the square in the denominator, we see that this is the Laplace transform of:
e. ...shifted by the rule:
f. Therefore, the solution is y=:
For the second question, i got Y(s) equals (39s+126)/(s^2(s+3)^2) but it says its wrong. The first one i got the answers except i dont know what rule they are referring too... Any help would be greatly appreciated.

Last edited by a moderator:
