logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
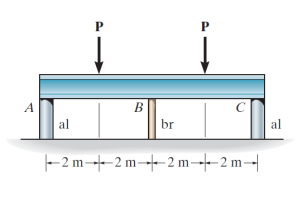
The rigid beam is supported by the three posts \(\displaystyle A, B,\) and \(\displaystyle C\). Posts \(\displaystyle A\) and \(\displaystyle C\) have a diameter of \(\displaystyle 60 \ \text{mm}\) and are made of \(\displaystyle \text{aluminum}\), for which \(\displaystyle E_{\text{al}} = 70 \ \text{GPa}\) and \(\displaystyle (\sigma_Y)_{\text{al}} = 20 \ \text{MPa}\). Post \(\displaystyle B\) is made of \(\displaystyle \text{brass}\), for which \(\displaystyle E_{\text{br}} = 100 \ \text{GPa}\) and \(\displaystyle (\sigma_Y)_{\text{br}} = 590 \ \text{MPa}\). If \(\displaystyle P = 130 \ \text{kN}\), determine the largest diameter of post \(\displaystyle B\) so that all the posts yield at the same time.