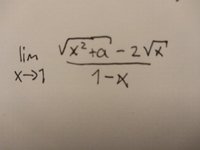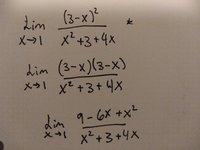You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Limit, unknown
- Thread starter Miriams
- Start date
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Miriams, is the given limit \(\displaystyle \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {{x^2} + a} - 2\sqrt x }}{{1 - x}}\)Find the number a so that the limit
View attachment 13910exists. Also find the limit for this situation.
Anyone who can explain how to find the answer?
OR IS it \(\displaystyle \mathop {\lim }\limits_{x \to 7} \frac{{\sqrt {{x^2} + a} - 2\sqrt x }}{{7 - x}}\)
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
The first thing I would do is note that, if we simply substitute x= 1, the denominator is 0. In order that this limit exist the numerator must also be 0. We must have \(\displaystyle \sqrt{1+ a}- 2= 0\). So \(\displaystyle \sqrt{1+ a}= 2\), 1+ a= 4, a= 3. Now do as pka suggested- multiply both numerator and denominator by \(\displaystyle \sqrt{x^2+ 3}+ 2\sqrt{x}\). (His final \(\displaystyle \sqrt{3}\)" appears to be a typo.)
It is the one where x->1Miriams, is the given limit \(\displaystyle \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {{x^2} + a} - 2\sqrt x }}{{1 - x}}\)
OR IS it \(\displaystyle \mathop {\lim }\limits_{x \to 7} \frac{{\sqrt {{x^2} + a} - 2\sqrt x }}{{7 - x}}\)
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
Thank you for the clarification. Now
\(\displaystyle \frac{\sqrt{x^2+a}-2\sqrt x}{1-x}\left(\frac{\sqrt{x^2+a}+2\sqrt x}{\sqrt{x^2+a}+2\sqrt x}\right)=\frac{(x^2+a)-4x}{(1-x)(\sqrt{x^2+a}+2\sqrt x)}\)
Now choose a value for \(\displaystyle a\) so you can factor \(\displaystyle x^2-4x+a=(x-1)(~?~)\)
Divide off the \(\displaystyle (x-1)\) and find the limit.
\(\displaystyle \frac{\sqrt{x^2+a}-2\sqrt x}{1-x}\left(\frac{\sqrt{x^2+a}+2\sqrt x}{\sqrt{x^2+a}+2\sqrt x}\right)=\frac{(x^2+a)-4x}{(1-x)(\sqrt{x^2+a}+2\sqrt x)}\)
Now choose a value for \(\displaystyle a\) so you can factor \(\displaystyle x^2-4x+a=(x-1)(~?~)\)
Divide off the \(\displaystyle (x-1)\) and find the limit.
Hmm, I am not sure what you meant in the last step. So we do not use L'hopitals rule?Thank you for the clarification. Now
\(\displaystyle \frac{\sqrt{x^2+a}-2\sqrt x}{1-x}\left(\frac{\sqrt{x^2+a}+2\sqrt x}{\sqrt{x^2+a}+2\sqrt x}\right)=\frac{(x^2+a)-4x}{(1-x)(\sqrt{x^2+a}+2\sqrt x)}\)
Now choose a value for \(\displaystyle a\) so you can factor \(\displaystyle x^2-4x+a=(x-1)(~?~)\)
Divide off the \(\displaystyle (x-1)\) and find the limit.
Last edited:
pka
Elite Member
- Joined
- Jan 29, 2005
- Messages
- 11,990
The limit is \(\displaystyle x\to 1\) so we have \(\displaystyle 0\) in the denominator. Thus we need to rid yourself of it.Hmm, I am not sure what you meant in the last step.
So we do not use L'hopitals rule? Absolutely not!
So what value of \(\displaystyle a\) would give us a factor \(\displaystyle (x-1)\) in the numerator?
If you have \(\displaystyle (x-1)\) in the numerator and \(\displaystyle (1-x)\) in the denominator thy divide to \(\displaystyle -1\).
Now as \(\displaystyle x\to 1\) the limit is defined. So \(\displaystyle a=~?\).
Do some work for yourself. We are not here to do your work for you.
- Joined
- Nov 24, 2012
- Messages
- 3,021
It is the one where x->1
Okay, so we need:
[MATH]\sqrt{1^2+a}-2\sqrt{1}=0[/MATH]
[MATH]\sqrt{a+1}=2[/MATH]
[MATH]a+1=4[/MATH]
[MATH]a=3[/MATH]
So we now have:
[MATH]L=\lim_{x\to1}\frac{\sqrt{x^2+3}-2\sqrt{x}}{1-x}[/MATH]
We could use L'Hôpital's rule since we have the indeterminate form 0/0, but let's rationalize the numerator:
[MATH]L=\lim_{x\to1}\frac{\sqrt{x^2+3}-2\sqrt{x}}{1-x}\cdot\frac{\sqrt{x^2+3}+2\sqrt{x}}{\sqrt{x^2+3}+2\sqrt{x}}[/MATH]
[MATH]L=\lim_{x\to1}\frac{x^2-4x+3}{(1-x)(\sqrt{x^2+3}+2\sqrt{x})}[/MATH]
[MATH]L=\lim_{x\to1}\frac{(x-1)(3-x)}{(x-1)(\sqrt{x^2+3}+2\sqrt{x})}[/MATH]
[MATH]L=\lim_{x\to1}\frac{3-x}{\sqrt{x^2+3}+2\sqrt{x}}[/MATH]
Can you proceed?
I tried this, but if I substitute the x with 1, there is no longer zero in the numerator and the denominatorOkay, so we need:
[MATH]\sqrt{1^2+a}-2\sqrt{1}=0[/MATH]
[MATH]\sqrt{a+1}=2[/MATH]
[MATH]a+1=4[/MATH]
[MATH]a=3[/MATH]
So we now have:
[MATH]L=\lim_{x\to1}\frac{\sqrt{x^2+3}-2\sqrt{x}}{1-x}[/MATH]
We could use L'Hôpital's rule since we have the indeterminate form 0/0, but let's rationalize the numerator:
[MATH]L=\lim_{x\to1}\frac{\sqrt{x^2+3}-2\sqrt{x}}{1-x}\cdot\frac{\sqrt{x^2+3}+2\sqrt{x}}{\sqrt{x^2+3}+2\sqrt{x}}[/MATH]
[MATH]L=\lim_{x\to1}\frac{x^2-4x+3}{(1-x)(\sqrt{x^2+3}+2\sqrt{x})}[/MATH]
[MATH]L=\lim_{x\to1}\frac{(x-1)(3-x)}{(x-1)(\sqrt{x^2+3}+2\sqrt{x})}[/MATH]
[MATH]L=\lim_{x\to1}\frac{3-x}{\sqrt{x^2+3}+2\sqrt{x}}[/MATH]
Can you proceed?
Attachments
Yes I agree with you. I meant the number is unknown. I don't know how to change it."unknown" - This is a troublesome word. It would have to mean that there IS a limit, but you just don't know it.
This is very much different from "there is no limit" or "the limit does not exist".
Yes, that is the same as I got when I exchanged the x with 1. But is this the final answer? We didn't need to derivate?I don't know where the expression you're working with came from.
If you continue from where I left off, you will find:
[MATH]L=\frac{3-1}{\sqrt{1^2+3}+2\sqrt{1}}=\frac{2}{2+2}=\frac{1}{2}[/MATH]
- Joined
- Nov 24, 2012
- Messages
- 3,021
Yes, that is the same as I got when I exchanged the x with 1. But is this the final answer? We didn't need to derivate?
Yes, that's the value of the limit. Like I said, we could also have applied L'Hôpital's rule:
[MATH]L=\lim_{x\to1}\frac{\sqrt{x^2+3}-2\sqrt{x}}{1-x}=\lim_{x\to1}\frac{\dfrac{x}{\sqrt{x^2+3}}-\dfrac{1}{\sqrt{x}}}{-1}=\frac{1}{2}[/MATH]
But, since we algebraically manipulated the expression so that it was no longer an indeterminate form, we could use direct substitution.
[MATH][/MATH]
Oh, now I understand. Thank you so much for the help! | ||||||
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
?? That's a GOOD thing, isn't it? You don't want a zero in the denominator!I tried this, but if I substitute the x with 1, there is no longer zero in the numerator and the denominator