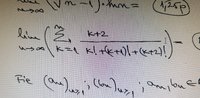You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Limits
- Thread starter Luca Gvr
- Start date
D
Deleted member 4993
Guest
Use:I need help with the following limit
k! + (k+1)! = k! * (k+2)
simplify the denominator.
AmandasMathHelp
New member
- Joined
- Feb 9, 2021
- Messages
- 35
It might help to know why the above works.. basically you are factoring out a k! out of both terms.
[MATH]k! + (k+1)! = k! + (k+1)*k!= k!* (1+k+1)[/MATH]
You can apply that idea to the entire bottom of the fraction. Then you'll be able to simply stuff after that. The following limit may be helpful . It's likely you do not need to prove this fact because the proof is a bit difficult.
. It's likely you do not need to prove this fact because the proof is a bit difficult.
[MATH] \sum_{n=1}^{\infty} \frac{1}{n!} = e [/MATH]
[MATH]k! + (k+1)! = k! + (k+1)*k!= k!* (1+k+1)[/MATH]
You can apply that idea to the entire bottom of the fraction. Then you'll be able to simply stuff after that. The following limit may be helpful
[MATH] \sum_{n=1}^{\infty} \frac{1}{n!} = e [/MATH]
AmandasMathHelp said:[MATH] \sum_{n=1}^{\infty} \frac{1}{n!} = e [/MATH]
That sum equals \(\displaystyle \ e - 1. \ \ \) You need to start with n = 0.
AmandasMathHelp
New member
- Joined
- Feb 9, 2021
- Messages
- 35
Ohhhh yep. My mistake