Line between two circle tangents

[Cato]

Hello,

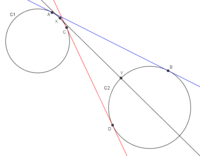
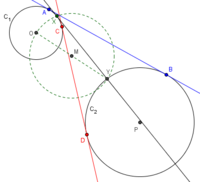
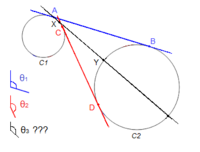
I have two circles C1 and C2. The outer tangent from C1 to C2 is the blue line that touches points A and B. The inner tangent from C1 to C2 is the red line that touches points C and D. I already have these points calculated (and their subsequent angles) using the tangent theorem.

However, I do not know how to find the straight line that cuts right between the outer and inner tangents, as approximated by the black line XY. It appears to me that point Y should be midway between B and D, and it follows that point X should be midway between A and C, but I am not sure.

Can I get these points (and subsequent angle θ3) simply by knowing the inner and outer tangents? Any help would be much appreciated.

 

[tkhunny]

I REALLY want to construct perpendicular bisectors at B and D in order to establish the center of C2. I'm not sure that will lead anywhere; it just kept bugging me for some reason. I'm not quite as tempted to do the same with A, C, and C1.

If you can use the tangent theorem to calculate the angle between AB and CD? Can't you use the same idea to calculate the angle from AB to XY and make sure it is the same as XY to CD?

Awesome drawing and explanation, BTW.

 

[Cato]

I REALLY want to construct perpendicular bisectors at B and D in order to establish the center of C2. I'm not sure that will lead anywhere; it just kept bugging me for some reason. I'm not quite as tempted to do the same with A, C, and C1.

If you can use the tangent theorem to calculate the angle between AB and CD? Can't you use the same idea to calculate the angle from AB to XY and make sure it is the same as XY to CD?

Awesome drawing and explanation, BTW.

I'm glad you like the drawing. I also thought about the perpendicular bisectors but I don't see how it helps the problem.

I should also explain that when I say I found the angles θ1 and θ2, I mean to say the actual vectors (AB) and (CD) converted into angles. I did not find the angle between AB and CD, if that makes sense. I don't know if that is even possible since they do not have the same point or origin.

I've searched online for hours, looking for secants between inner and outer tangents, but I can't seem to find anything. Is this really a rare problem?!

 

[Dr.Peterson]

I do not know how to find the straight line that cuts right between the outer and inner tangents, as approximated by the black line XY.

Please define what this means. Clearly you don't mean the angle bisector; so what do you mean? Is it required to be tangent to C1? And if it is only approximated by XY, what about it may be different from XY?

 

[Cato]

Please define what this means. Clearly you don't mean the angle bisector; so what do you mean? Is it required to be tangent to C1? And if it is only approximated by XY, what about it may be different from XY?

Sorry if I wasn't clear. Yes it must be tangent to C1 and it must pass through C2 precisely in between B and D. I hope that makes it clearer?

I said approximated because I sketched the lines and points roughly, in reality point X and Y may not be exactly where I placed them.

 

[Dr.Peterson]

Sorry if I wasn't clear. Yes it must be tangent to C1 and it must pass through C2 precisely in between B and D. I hope that makes it clearer?

I said approximated because I sketched the lines and points roughly, in reality point X and Y may not be exactly where I placed them.

Part of the reason I asked was that you said:

It appears to me that point Y should be midway between B and D

That sounds like a guess rather than a known requirement.

But you're probably right not to be sure that:

it follows that point X should be midway between A and C, but I am not sure.

Another uncertainty is how you want to find this line. Do you have coordinates and radii and want to find an equation of the line, or do you want to construct with compass and straightedge, or what?

 

[Cato]

Another uncertainty is how you want to find this line. Do you have coordinates and radii and want to find an equation of the line, or do you want to construct with compass and straightedge, or what?

Okay so I already know the following information:

- Co-ordinate of A (x, y)
- Co-ordinate of B (x, y)
- Co-ordinate of C (x, y)
- Co-ordinate of D (x, y)
- θ1 (from Vector AB)
- θ2 (from Vector CD)
- Radius of C1
- Radius of C2
- Distance between centres of circles

My ultimate objective is to find θ3. If this means having to find co-ordinates of X and Y, so be it. Or if there is another way just by using θ1 and θ2 then that’s fine too. Once I know the maths I will be translating it into C code, as this is ultimately for a computer program. So using a hand drawn solution is not really suitable.

 

[Dr.Peterson]

Here's my first thought:

From A and C and r1, find the center O of C1.​

​

From B and D and r2, find the center P of C2.​

​

Bisect arc BD to find Y.​

​

Now you need to find X, the point of tangency for a tangent from Y to C1. This, of course, is what you're asking how to do. That part is easy with a compass and straightedge: find the midpoint of OY, make the circle with its center there passing through O and Y, and intersect that with C1 to find X. You can translate that into equations.​

Then I tried playing with this in GeoGebra, and found that the problem is overspecified -- you have far too much information, which could easily be inconsistent. In fact, not all sets of points A, B, C, and D will work. (You already know, it seems, that the two angles are derived from the known points, so they shouldn't be listed separately as givens.)

For example, I could construct the figure, using just the two known tangent lines and the two radii. All the rest can be derived from that. Here's the result:



Alternatively, you could start with the two circles (that is, O, P, and the radii), and find the four points of tangency. Maybe that's what you really did.

But given that you know the correct coordinates of A, B, C, and D, from whatever source, my procedure above would work.

 

[jonah2.0]

Beer induced request follows.

Okay so I already know the following information:

- Co-ordinate of A (x, y)
- Co-ordinate of B (x, y)
- Co-ordinate of C (x, y)
- Co-ordinate of D (x, y)
- θ1 (from Vector AB)
- θ2 (from Vector CD)
- Radius of C1
- Radius of C2
- Distance between centres of circles
...

Can you please state them in the cartesian coordinate system if possible?
It would be very helpful for those of us closely following this thread.

 

[Cato]

Alternatively, you could start with the two circles (that is, O, P, and the radii), and find the four points of tangency. Maybe that's what you really did.

Your diagram is much clearer so a big thanks for that! And yes you are absolutely correct - I started by finding the four points of tangency (A,B,C,D). I do already know the central co-ordinates (O, P) of both circles, my apologies for forgetting to list that.

My problem lies precisely with translating your process into equations; I do not know how to find X and Y using trigonometric functions. In light of knowing O and P, is this possible? My apologies if I am missing something obvious here.

 

[Cato]

Can you please state them in the cartesian coordinate system if possible?
It would be very helpful for those of us closely following this thread.

Sure here is a set of co-ordinates from the illustrated scenario. These are from a computer simulation so I have tried to approximate their position relative the x and y axes as close as I could (bottom left of the JPEG is (0,0)).

- A (1.60, 4.22)
- B (5.02, 2.80)
- C (2.14, 3.69)
- D (3.25, 1.03)

- Radius C1 = 1
- Radius C2 = 1.35
- C1 Centre (1.22, 3.3)
- C2 Centre (4.50, 1.55)

- θ1 = 112.68°
- θ2 = 157.29°

 

[Dr.Peterson]

My problem lies precisely with translating your process into equations; I do not know how to find X and Y using trigonometric functions. In light of knowing O and P, is this possible? My apologies if I am missing something obvious here.

I can't be sure what should be obvious, because it isn't clear how much you know about trigonometry or algebra.



Finding Y should be easy. You could use vectors PB and PD and add them to find the direction of PY, for example. Once you have that direction, just scale the vector to get PY.

Then, as I said, you can find the midpoint of OY (just average the coordinates), then find the equation of the circle with that center through O, and intersect that with C1.

None of this is trivial, but it's all "obvious" what to do, from what I've already said. Of course, others may suggest a more efficient way; I haven't tried actually carrying that out to see if anything gets difficult.

 

[Cato]

Finding Y should be easy. You could use vectors PB and PD and add them to find the direction of PY, for example. Once you have that direction, just scale the vector to get PY.

Thank you so much, following your method I have been to plot Point Y.

Then, as I said, you can find the midpoint of OY (just average the coordinates), then find the equation of the circle with that center through O, and intersect that with C1.

In terms of finding X, could you please elaborate on this point as I'm not sure what you mean. Which co-ordinates do you mean to average?

 

[Dr.Peterson]

In terms of finding X, could you please elaborate on this point as I'm not sure what you mean. Which co-ordinates do you mean to average?

Do you not know the midpoint formula?

The coordinates of the midpoint of segment OY are the average of the coordinates of O and Y. See the link for examples.

 

[Cato]

Do you not know the midpoint formula?

The coordinates of the midpoint of segment OY are the average of the coordinates of O and Y. See the link for examples.

Dr.Peterson, I followed your method and it has enabled me to successfully plot both Point X and Y and find the subsequent angle of the vector XY (θ3)! Thank you so much.

I have a question though, can we be confident that the line XY truly is tangent to c1? I took the point of intersection as you outlined, and I trust your method. But I am wondering how certain we can be on the tangency?

 

[Dr.Peterson]

I have a question though, can we be confident that the line XY truly is tangent to c1? I took the point of intersection as you outlined, and I trust your method. But I am wondering how certain we can be on the tangency?

The construction guarantees that it is tangent. First, X is on the circle; second, triangle OXY, being inscribed in a semicircle, is a right triangle, so the line XY is perpendicular to the radius OX. That makes it tangent. And that's why I used that circle! It's a standard construction for a tangent.

 

[Cato]

The construction guarantees that it is tangent. First, X is on the circle; second, triangle OXY, being inscribed in a semicircle, is a right triangle, so the line XY is perpendicular to the radius OX. That makes it tangent. And that's why I used that circle! It's a standard construction for a tangent.

Just what I needed to hear. You have solved my problem, I cannot thank you enough!

What's best is that you helped me to understand the method so I could perform that calculations myself. Much appreciated!